
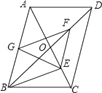
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
证明△BCO是等腰三角形即可证明①正确;由EG=![]() AB,EF=
AB,EF=![]() AB可证②成立;由中点的性质可得出EF∥CD,且EF=
AB可证②成立;由中点的性质可得出EF∥CD,且EF=![]() CD=BG,结合平行即可证得③结论成立;由三线合一可证明④成立;无法证明⑤成立;此题得解.
CD=BG,结合平行即可证得③结论成立;由三线合一可证明④成立;无法证明⑤成立;此题得解.
∵四边形ABCD是平行四边形,
∴BD=2BO,AD=BC,
∵BD=2AD,
∴BD=2BC,
∴BO=BC,
∵E为OC中点,
∴BE⊥AC,故①成立;
∵BE⊥AC,G是AB中点,
∴EG=![]() AB,
AB,
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=![]() CD,
CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴EF=![]() AB,
AB,
∴EF=EG,故②成立;
∵AB∥CD,EF∥CD,
∴EF∥AB,
∴∠FEG=∠BGE(两直线平行,内错角相等),
在△EFG和△GBE中,
∵BG=FE,∠FEG=∠BGE,GE=EG,
∴△EFG≌△GBE(SAS),即③成立;
∵BG=FE,EF∥AB,
∴四边形BEFG是平行四边形,
∵BE⊥AC,
∴GF⊥AC,
∵EF=EG,
∴∠AEG=∠AEF,
即EA平分∠GEF
故④正确,
若四边形BEFG是菱形
∴BE=BG=![]() AB,
AB,
∴∠BAC=30°
与题意不符合
故⑤错误
故选C.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况,研究:
(1)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②说明理由.
(2)三角板绕点P旋转,△PCE是否能成为等腰三角形?若能,指出所有情况(即写出△PCE为等腰三角形时BE的长);若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线l1:y=﹣x+n过点A(﹣1,3),双曲线C:y= ![]() (x>0),过点B(1,2),动直线l2:y=kx﹣2k+2(常数k<0)恒过定点F.
(x>0),过点B(1,2),动直线l2:y=kx﹣2k+2(常数k<0)恒过定点F.
(1)求直线l1 , 双曲线C的解析式,定点F的坐标;
(2)在双曲线C上取一点P(x,y),过P作x轴的平行线交直线l1于M,连接PF.求证:PF=PM.
(3)若动直线l2与双曲线C交于P1 , P2两点,连接OF交直线l1于点E,连接P1E,P2E,求证:EF平分∠P1EP2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
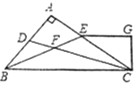
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG//BC,且![]() 于G,下列结论:①
于G,下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论是( )
;其中正确的结论是( )
A.只有①③B.只有①③④C.只有②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a0,a1,a2,a3,a4,…,满足下列条件:a0=0,a1=﹣|a0+1|,a2=﹣|a1+2|,a3=﹣|a2+3|,…,以此类推,a2019的值是( )
A. ﹣1009B. ﹣1010C. ﹣2018D. ﹣2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从数轴上的原点开始,先向左移动2cm到达A点,再向左移动4cm到达B点,然后向右移动10cm到达C点.
![]()
(1)用1个单位长度表示1cm,请你在题中所给的数轴上表示出A、B、C三点的位置;
(2)把点C到点A的距离记为CA,则CA=______cm;
(3)若点B以每秒3cm的速度向左移动,同时A、C点以每秒lcm、5cm的速度向右移动,设移动时间为t(t>0)秒,试探究CA﹣AB的值是否会随着t的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线![]() ⊥
⊥![]() 于点
于点![]() ,△
,△![]() 是直角三角形,且∠
是直角三角形,且∠![]() =90°,斜边
=90°,斜边![]() 交直线
交直线![]() 于点
于点![]() ,
,![]() 平分∠
平分∠![]() ,∠
,∠![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() ,∠
,∠![]() =36°.
=36°.
(1)如图1,当![]() ∥
∥![]() 时,求∠
时,求∠![]() 的度数.
的度数.
(2)如图2,当△![]() 绕
绕![]() 点旋转一定的角度(即
点旋转一定的角度(即![]() 与
与![]() 不平行),其他条件不变,问∠
不平行),其他条件不变,问∠![]() 的度数是否发生改变?请说明理由.
的度数是否发生改变?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com