
����Ŀ����ͼ���������ϵ�ԭ�㿪ʼ���������ƶ�2cm����A�㣬�������ƶ�4cm����B�㣬Ȼ�������ƶ�10cm����C�㣮
![]()
��1����1����λ���ȱ�ʾ1cm�����������������������ϱ�ʾ��A��B��C�����λ�ã�
��2���ѵ�C����A�ľ����ΪCA����CA��______cm��
��3������B��ÿ��3cm���ٶ������ƶ���ͬʱA��C����ÿ��lcm��5cm���ٶ������ƶ������ƶ�ʱ��Ϊt��t��0���룬��̽��CA��AB��ֵ�Ƿ������t�ı仯���ı䣿��˵�����ɣ�
���𰸡���1����ͼ��ʾ������������2��CA��6cm����3��CA��AB��ֵ��������t�ı仯���仯�����ɼ�����.
��������
��1�����������ϵ���ƶ����ɣ��������ϱ�ʾ��A��B��C��λ�ü��ɣ���2�����������������ľ��빫ʽ���CA�ij����ɣ���3�����ƶ�ʱ��Ϊt��ʱ����ʾ��A��B��C��ʾ���������CA-AB��ֵ���������жϣ�
��1����ͼ��ʾ��
![]()
��2��CA��4������2����4+2��6��cm����
�ʴ�Ϊ��6��
��3��CA��AB��ֵ��������t�ı仯���仯���������£�
��������ã�CA����4+5t��������2+t����6+4t��AB������2+t��������6��3t����4+4t��
��CA��AB����6+4t������4+4t����2��
��CA��AB��ֵ��������t�ı仯���仯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
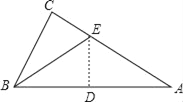
����Ŀ����һֱ��������ֽƬ����C��90����BC��6��AC��8���ֽ���ABC����ͼ�����۵���ʹ��A���B�غϣ��ۺ�ΪDE����CE�ij�Ϊ��������
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
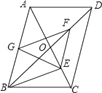
����Ŀ����ͼ��ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��BD��2AD��E��F��G�ֱ���OC��OD��AB���е㣬���н��ۣ���BE��AC����EG��EF������EFG�ա�GBE����EAƽ�֡�GEF�����ı���BEFG�����Σ�������ȷ�ĸ����ǣ�������
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���滮һ����70m����30m�ij����β�ƺ��������ͬ����������ʹ����������ABƽ�У���һ����BCƽ�У��������ಿ���ֲݣ����Ŀ���Ϊxm��
��1���ú�x�Ĵ���ʽ��ʾ��ƺ�������S��
��2�����ÿһ���ƺ���������ȣ������Ŀ�Ϊ1m����ôÿ���ƺ������Ƕ���ƽ���ף�����ȷ��0.1��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����5���ⳤΪ1�������������ͼ��ʾ�ļ����壮
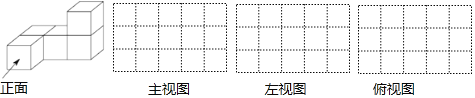
��1���ü����������Ƕ���������λ��������Ƕ���ƽ����λ���������������
��2�����ڷ���ֽ����ʵ��������������ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AGF=��ABC����1+��2=180�㣬
��1����֤��BF��DE��
��2�����DE��AC�ڵ�E����2=150�㣬���AFG�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪a��b����![]() +|b-1|=0����b-a������ƽ������
+|b-1|=0����b-a������ƽ������
��2�����һ������m������ƽ�����ֱ���2a��3��a��9����2m��2��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ����ǡ�ͬ����У�ΪŬ�������н��ɡ������ֳ��С����̻���˾�ƻ�����A��B��C�����̻�����800�꣬��20������һ���˻أ������г����½���·�����̻������ƻ���20��������Ҫװ�ˣ�ÿ������ֻ��װ��ͬһ���̻������ұ���װ���������±��ṩ����Ϣ������������⣺
�� �� �� Ʒ �� | A | B | C |
ÿ���������������꣩ | 40 | 48 | 32 |
ÿ������ļ۸�Ԫ�� | 20 | 50 | 30 |
��1����װ��A���̻����ij�����Ϊx��װ��B���̻����ij�����Ϊy����y��x֮��ĺ�����ϵʽ��
��2�����װ��ÿ���̻����ij�������������8������ô�����İ��ŷ����м��֣���д��ÿ�ְ��ŷ�����
��3�����ڡ����ǡ�ͬ�����Ҫ�����н�Լ����ʵ�£���Ӧ���ã�2���е����ְ��ŷ�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������A��B��C�������Ӧ�����ֱ���a��b��c��������|a+24|+|b+10|+��c-10��2=0������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮
![]()
��1����a��b��c��ֵ��
��2������P��A������ǵ�B������2�������P�Ķ�Ӧ������
��3������P�˶���B��ʱ����Q��A���������ÿ��2����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A���ڵ�Q��ʼ�˶���ڼ���ʱ��P��Q����֮��ľ���Ϊ8����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com