Question

11．（1）解方程：$\frac{x}{x-2}$=$\frac{2}{x-2}$-1
（2）如图△ABD是直角三角形，∠B=90°，E是BD上一点，过点D作DC⊥AE交AE的延长线于点C，AE=4，DE=2．DC=$\frac{8}{5}$
填空：△ADE的边DE上的高是线段AB，边AE上的高是线段DC．
线段AB的长为$\frac{16}{5}$．

Answer 1

分析 （1）直接利用解分式方程的方法去分母解方程即可；
（2）利用三角形的高线的定义结合相似三角形的判定与性质求出AB的长．

解答 解：（1）去分母得：x=2-（x-2）
解得：x=2．
检验：把x=2代入x-2得x-2=0，
所以原方程无解．

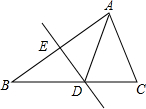
（2）∵过点D作DC⊥AE交AE的延长线于点C，∠B=90°，
∴△ADE的边DE上的高是线段AB，边AE上的高是线段DC，
∵∠B=∠C，∠AEB=∠CED，
∴△ABE∽△DCE，
∴$\frac{AB}{DC}$=$\frac{AE}{DE}$，
∵AE=4，DE=2．DC=$\frac{8}{5}$，
∴$\frac{AB}{\frac{8}{5}}$=$\frac{4}{2}$，
解得：AB=$\frac{16}{5}$．
故答案为：AB，DC，$\frac{16}{5}$．

点评 此题主要考查了解分式方程以及相似三角形的判定与性质，正确得出△ABE∽△DCE是解题关键．