
【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处. 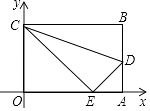
(1)求点E的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F. ①求△COF的面积;
②在x轴上是否存在点P,使S△OCP= ![]() S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)解:∵四边形ABCD是长方形,
∴BC=OA=10,∠COA=90°,
由折叠的性质知,CE=CB=10,
∵OC=6,
∴在直角△COE中,由勾股定理得OE= ![]() =8,
=8,
∴E(8,0)
(2)解:设CD所在直线的解析式为y=kx+b(k≠0),
∵C(0,6),
∴b=6,
设BD=DE=x,
∴AD=6﹣x,AE=OA﹣OE=2,
由勾股定理得AD2+AE2=DE2
即(6﹣x)2+22=x2,
解得x= ![]() ,
,
∴AD=6﹣ ![]() =
= ![]() ,
,
∴D(10, ![]() ),
),
代入y=kx+6 得,k=﹣ ![]() ,
,
故CD所在直线的解析式为:y=﹣ ![]() x+6
x+6
(3)解:①在y=﹣ ![]() x+6中,令y=0,则x=18,
x+6中,令y=0,则x=18,
∴F(18,0),
∴△COF的面积= ![]() ×OF×OC=
×OF×OC= ![]() ×18×6=54;
×18×6=54;
②在x轴上存在点P,使得S△OCP= ![]() S△COF,
S△COF,
设P(x,0),依题意得
![]() ×OP×OC=
×OP×OC= ![]() ×54,即
×54,即 ![]() ×|x|×6=18,
×|x|×6=18,
解得x=±6,
∴在x轴上存在点P,使得S△OCP= ![]() S△COF,点P的坐标为(6,0)或(﹣6,0).
S△COF,点P的坐标为(6,0)或(﹣6,0).
【解析】(1)根据折叠的性质知CE=CB=10.在在直角△COE中,由勾股定理求得OE=8;(2)根据OC=6知C(0,6),由折叠的性质与勾股定理,求得D(10, ![]() ),利用待定系数法求CD所在直线的解析式;(3)①根据F(18,0),即可求得△COF的面积;②设P(x,0),依S△OCP=
),利用待定系数法求CD所在直线的解析式;(3)①根据F(18,0),即可求得△COF的面积;②设P(x,0),依S△OCP= ![]() S△CDE得
S△CDE得 ![]() ×OP×OC=
×OP×OC= ![]() ×54,即
×54,即 ![]() ×|x|×6=18,求得x的值,即可得出点P的坐标.
×|x|×6=18,求得x的值,即可得出点P的坐标.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣2)3﹣( ![]() )﹣1+(
)﹣1+( ![]() ﹣1)0+(﹣
﹣1)0+(﹣ ![]() )2017×(1.5)2016
)2017×(1.5)2016
(2)(2a+1)(2a﹣1)﹣(a+2)2﹣3a(a+1)
(3)( ![]() ﹣1)÷
﹣1)÷ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误. 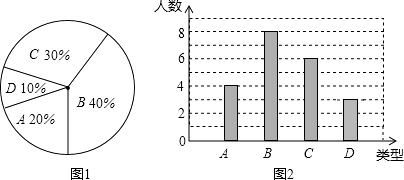
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的: 
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
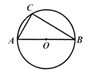
【题目】(10分)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,![]() 所围成区域的面积.(其中
所围成区域的面积.(其中![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°. 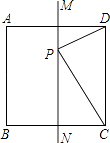
A.60°
B.45°
C.30°
D.15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将n个边长都为1cm的正方形按如图所示的方法摆放,点A1 , A2 , …,An分别是正方形对角线的交点,则n个正方形重叠形成的重叠部分的面积和为( )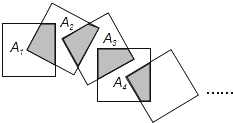
A.![]() cm2
cm2![]()
B.![]() cm2
cm2![]()
C.![]() cm2
cm2![]()
D.( ![]() )ncm2
)ncm2
查看答案和解析>>
科目:初中数学 来源: 题型:
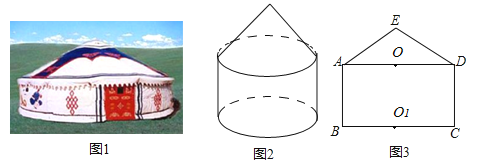
【题目】图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.
(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.随意翻到一本书的某页,页码是奇数
B.抛掷一枚普通硬币,正面朝下
C.抛得一枚普通正方体般子所得点数大于3
D.太阳每天从东方升起
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com