
【题目】(10分)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E.求出由线段ED,BE,![]() 所围成区域的面积.(其中
所围成区域的面积.(其中![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
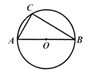
【答案】(1)作图见解析;(2)30°;(3)![]() .
.
【解析】
试题分析:(1)作AP平分∠CAB交⊙O于D;
(2)由等腰三角形性质得到∠CAD=∠ADC.又由∠ADC=∠B,得到∠CAD=∠B.
再根据角平分线定义得到∠CAD=∠DAB=∠B.由于直径所对圆周角为90°,得到∠ACB=90°,从而得到∠B的度数;
(3)先得到△OEB是30°角的直角三角形,从而得出OE,EB的长,然后把不规则图形面积转化为扇形BOD的面积减去Rt△OEB的面积求解.
试题解析:(1)如图,AP即为所求的∠CAB的平分线;
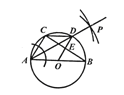
(2)∵AC=CD,∴∠CAD=∠ADC.又∵∠ADC=∠B,∴∠CAD=∠B.
∵AD平分∠CAB,∴∠CAD=∠DAB=∠B.
∵AB是⊙O的直径,∴∠ACB=90°,∴∠CAB+∠B=90°,∴3∠B=90° ,∴∠B=30°;
(3)由(2)知,∠DAB=30°.又∵∠DOB=2∠DAB,∴∠EOB=60°,∴∠OEB=90°.
在Rt△OEB中,∵OB=4,∠OBE=30°,∴OE=2,BE=![]() ,∴S=
,∴S=![]() =
=![]() =
=![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】下列关系中的两个量成正比例的是( )
A. 从甲地到乙地,所用的时间和速度
B. 正方形的面积与边长
C. 买同样的作业本所要的钱数和作业本的数量
D. 人的体重与身高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③a<![]() ;④b>1.其中正确的结论是( )
;④b>1.其中正确的结论是( )
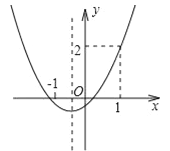
A.①② B.②③ C.③④ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
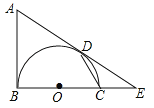
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=27°,OB=2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处. 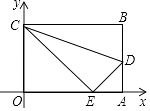
(1)求点E的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F. ①求△COF的面积;
②在x轴上是否存在点P,使S△OCP= ![]() S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C、D是平面直角坐标系中坐标轴上的点,且△AOB≌△COD,设直线AB的表达式为y1=ax+b,直线CD的表达式为y2=mx+n,则am= . 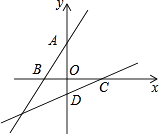
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;
(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).
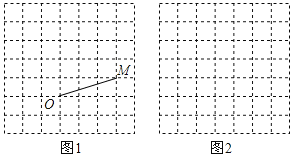
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com