
【题目】射阳火车站是连盐铁路(已与青连铁路合并为青盐铁路)沿线的一个县级车站,位于江苏省射阳县海河镇条海村,射阳站的建成结束了射阳县无铁路的历史。设正在行驶途中的某一时刻,记为T时刻,铁路上(双轨)迎面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD=4(单位长度),如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是b.若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,且![]() .
.
(1)求此时刻快车头A与慢车头C之间相距多少单位长度?
(2)如果此时刻将数轴折叠,使点A与点C重合,则点B与数轴上表示数_____的点重合。
(3)若在T时刻,一架无人机正在B的正上方以10个单位长度/秒的速度向右匀速飞行,则问当它飞到A的正上方时,求此时AC之间的距离?
(4)从T时刻开始算起,问再行驶多少秒钟两列火车行驶到车头AC相距8个单位长度?
(5)在T时刻,快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟,他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值(即PA+PC+PB+PD为定值).你认为学生P发现的这一结论是否正确?若正确,求出这个时间及定值;若不正确,请说明理由.
![]()
【答案】(1)16个单位长度;(2)8;(3)12个单位长度;(4)1秒或3秒;(5)正确,这个时间是0.5秒,定值是6个单位长度.
【解析】
(1)根据非负数的性质可求出a,b,从而得到快车头A与慢车头C之间的距离;
(2)首先求出AC的中点以及点B表示的数,根据中点公式列方程求解即可;
(3)首先求出无人机飞到A的正上方所需的时间,然后可计算AC之间的距离;
(4)分两种情况讨论:①相遇前,②相遇后,分别根据时间=路程÷速度和,列式计算即可;
(5)由于PA+PB=AB=2,故只需要满足PC+PD是定值,从快车AB上乘客P与慢车CD相遇到完全离开之间都满足PC+PD是定值,依此分析即可求解.
解:(1)∵![]() ,
,
∴a+10=0,b-6=0,
∴a=-10,b=6,
∵6-(-10)=16,
∴此时刻快车头A与慢车头C之间相距16个单位长度;
(2)∵点A表示的数为-10,点C表示的数为6,
∴ AC的中点为![]() ,
,
而点B表示的数为:-10-2=-12,
设折叠后与点B重合的点表示的数为x,
则![]() ,
,
解得:x=8,
故将数轴折叠,使点A与点C重合,则点B与数轴上表示数8的点重合;
(3)设经过t秒无人机飞到A的正上方,
由题意得:(10-6)t=2,
解得:t=![]() ,
,
故此时AC之间的距离为:16-(6+2)×![]() =12(单位长度);
=12(单位长度);
(4)分两种情况讨论,
①相遇前车头AC相距8个单位长度,
由题意得:(16-8)÷(6+2)=1(秒);
②相遇后车头AC相距8个单位长度,
由题意得:(16+8)÷(6+2)=3(秒);
故再行驶1秒或3秒两列火车行驶到车头AC相距8个单位长度;
(5)正确,
∵PA+PB=AB=2,
∴当P在CD之间时,PC+PD是定值4,
∴t=4÷(6+2)=4÷8=0.5(秒),
此时PA+PC+PB+PD=(PA+PB)+(PC+PD)=2+4=6(单位长度).
故这个时间是0.5秒,定值是6个单位长度.


科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,![]() D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且![]() 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF
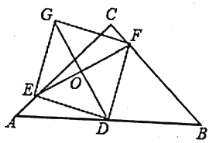
(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾(其中A、B、C、D分别表示可回收物、厨余垃圾、有害垃圾和其它垃圾)的分类情况,进行整理后,绘制了如下两幅尚不完整的统计图.试根据图表解答下列问题:

(1)请将图①中的条形统计图补充完整;
(2)在图②中的扇形统计图中,“D”部分所对应的圆心角等于 度;
(3)在抽样数据中,产生的有害垃圾共有多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把大于1的正整数![]() 的三次幂按一定规则“分裂”成若干个连续奇数的和,如
的三次幂按一定规则“分裂”成若干个连续奇数的和,如![]() ,
,![]() ,
,![]() ,…若
,…若![]() 分裂后,其中有一个奇数是2019,则
分裂后,其中有一个奇数是2019,则![]() 的值是( )
的值是( )
A.44B.45C.46D.47
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念学习)
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,一般地,把![]() (a≠0)记作a,读作“a的圈n次方”.
(a≠0)记作a,读作“a的圈n次方”.
(初步探究)
(1)直接写出计算结果:2③=_____,(﹣![]() )⑤=_____.
)⑤=_____.
(2)关于除方,下列说法准确的选项有_________(只需填入正确的序号)
①.任何非零数的圈2次方都等于1; ②.对于任何正整数n,1=1;
③.3④=4③ ④.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
(深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
例如: 2④=2÷2÷2÷2
=2×![]() ×
×![]() ×
×![]()
=(__)2 (幂的形式)
试一试:将下列除方运算直接写成幂的形式.
5⑥=_____;(﹣![]() )⑩=_____;a=_____(a≠0).
)⑩=_____;a=_____(a≠0).
算一算:![]() ④÷23+(﹣8)×2③.
④÷23+(﹣8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).

(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC=![]() .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com