练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知x，y是有理数，且（1+$\sqrt{3}$）x+（1-$\sqrt{3}$）y-12=0，求x，y的值．

    分析 已知等式整理后，确定出x与y的值即可．

    解答 解：已知等式整理得：（x+y）$\sqrt{3}$+x-y-12=0，
    可得$\left\{\begin{array}{l}{x+y=0}\\{x-y-12=0}\end{array}\right.$，
    解得：$\left\{\begin{array}{l}{x=6}\\{y=-6}\end{array}\right.$．

    点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．设x1，x2是方程x2-2x-1=0的两个实数根，则$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$的值是（　　）
    A．-6B．-5C．-6或-5D．6或5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

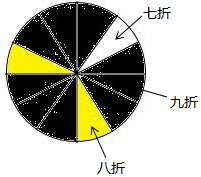    8．某商场为了吸引顾客，开展了一种转动转盘打折促销的话动，顾客在该商场同一日消费300-1000元时，就可获得一次转动转盘的机会，当转盘停止转动时，指针指向几折（指针落在分界线上时，重新转动一次），顾客就按几折价格付款，消费在1000元以上时，顾客可获得二次转动转盘的机会，顾客可按折上折付款．
    （1）小明的妈妈消费650元，求她获得打七折的机会的概率；
    （2）小丽的妈妈消费了1200元，请你用画树状图或列表的方法，求她获得折上折且都是七折的机会的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．求下列各式有意义的字母的取值范围．
    （1）$\sqrt{3x-4}$；（2）$\frac{\sqrt{2x+1}}{1-|x|}$；（3）$\sqrt{{m}^{2}+4}$；（4）$\sqrt{\frac{1}{x}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知a+b=4，ab=2，则$\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}$的值等于2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，已知y=kx和双曲线y=$\frac{m}{x}$（m＞0），点A（a，b）（a＞0）在双曲线y=$\frac{m}{x}$上
    （1）当a=b=2时，①直接写出m值4
    ②若k=-2，将直线y=kx平移至双曲线y=$\frac{m}{x}$只有一个交点，求平移后的直线解析式
    （2）将直线y=kx绕怨念O旋转，设旋转后直线与双曲线y=$\frac{m}{x}$交于B、C两点（点B在第一象限）直线AB、AC分别与x轴交于D、E两点，写出$\frac{AB}{AD}$与$\frac{AC}{AE}$之间的数量关系？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．若两条抛物线的顶点相同，则称它们为“友好抛物线”，已知抛物线C1：y1=-x2+ax+b与抛物线C2：y2=2x2+4x+6为“友好抛物线”，抛物线C1与x轴交于点A、C，与y轴交于点B．
    （1）求抛物线C1的表达式．
    （2）若F（t，0）（-3＜t＜0）是x轴上的一点，过点F作x轴的垂线交抛物线与点P，交直线AB于点E，过点P作PD⊥AB于点D．
    ①是否存在点F，使PE+PD的值最大，若存在，请求出t的值；若不存在，请说明理由．
    ②连接PA，以AP为边作图示一侧的正方形APMN，随着点F的运动，正方形的大小、位置也随之改变．当正方形APMN中的边MN与y轴有且仅有一个交点时，求t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，在平面直角坐标系中，点A，B的坐标分别为（0，3）和（9，0），若坐标轴上存在点C，使△OBC和△OAB相似，则点C的坐标是（-9，0）（1，0）（-1，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在平面直角坐标系xOy中，对于线段MN的“三等分变换”，给出如下定义：如图1，点P，Q为线段MN的三等分点，即MP=PQ=QN，将线段PM以点P为旋转中心顺时针旋转90°得到PM′，将线段QN以点Q为旋转中心顺时针旋转90°得到QN′，则称线段MN进行了三等分变换，其中M′，N′记为点M，N三等分变换后的对应点．
    例如：如图2，线段MN，点M的坐标为（1，5），点N的坐标为（1，2），则点P的坐标为（1，4），点Q的坐标为（1，3），那么线段MN三等分变换后，可得：M′的坐标为（2，4），点N′的坐标为（0，3）．

    （1）若点P的坐标为（2，0），点Q的坐标为（4，0），直接写出点M′与点N′的坐标；
    （2）若点Q的坐标是（0，-$\frac{\sqrt{2}}{2}$），点P在x轴正半轴上，点N′在第二象限．当线段PQ的长度为符合条件的最小整数时，求OP的长；
    （3）若点Q的坐标为（0，0），点M′的坐标为（-3，-3），直接写出点P与点N的坐标；
    （4）点P是以原点O为圆心，1为半径的圆上的一个定点，点P的坐标为（$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）当点N′在圆O内部或圆上时，求线段PQ的取值范围及PQ取最大值时点M′的坐标．

    查看答案和解析>>

    同步练习册答案