
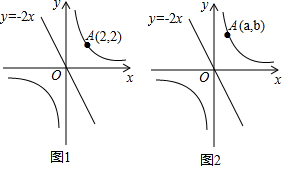
分析 (1)①把A(2,2)代入y=$\frac{m}{x}$即可得到结论;②设平移后的直线为y=-2x+b,解方程组即可得到结论;
(2)当点A在直线BC的上方,过A,B,C分别作y轴的垂线,垂足为F,G,H,则OF=b,OG=OH=n,FG=OF-OG=b-n,FH=OF+OH=b+n根据平行线分线段成比例定理即可得到结论.
解答 解:(1)①把A(2,2)代入y=$\frac{m}{x}$得,m=4,
故答案为:4;
②设平移后的直线为y=-2x+b,
∴$\left\{\begin{array}{l}{y=-2x+b}\\{y=\frac{4}{x}}\end{array}\right.$,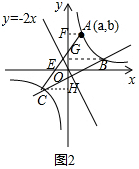
∴2x2-bx+4=0,
∵△=(-b)2-4×2×4=0,
∴b=4$\sqrt{2}$,
方程有两个相等的实数根,此时直线y=-2x+b曲线y=$\frac{m}{x}$只有一个交点,
∴平移后的直线为y=-2x+4$\sqrt{2}$;
(2)当点A在直线BC的上方,过A,B,C分别作y轴的垂线,垂足为F,G,H,
则OF=b,OG=OH=n,FG=OF-OG=b-n,FH=OF+OH=b+n,
∵AF∥x轴∥CH,
∴$\frac{AC}{AE}=\frac{FH}{FO}$=$\frac{b+n}{b}$,
∴$\frac{AC}{AE}+\frac{AB}{AD}$=$\frac{b+n}{b}$+$\frac{b-n}{b}$=2;
当A在BC的下方时,同理可求$\frac{AB}{AD}$=$\frac{n-b}{b}$,$\frac{AC}{AE}$=$\frac{n+b}{b}$,
∴$\frac{AC}{AE}$-$\frac{AB}{AD}$=2,
综上所述,$\frac{AC}{AE}$±$\frac{AB}{AD}$=2.
点评 本题考查了坐标与图形变换-旋转,待定系数法求函数的解析式,平行线分线段成比例定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
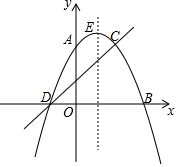 如图,抛物线y=ax2+bx+c过A(0,4),B(4,0),C(2,4)三点,与x轴另一交点记作D,直线y=kx+n过C、D两点.
如图,抛物线y=ax2+bx+c过A(0,4),B(4,0),C(2,4)三点,与x轴另一交点记作D,直线y=kx+n过C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
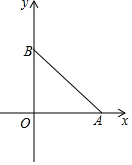 如图,在平面直角坐标系中,点O为坐标原点,A(a,0),B(0,b),且a,b满足(a-4)2+|b-4|=0,连接AB,∠OBA=45°.
如图,在平面直角坐标系中,点O为坐标原点,A(a,0),B(0,b),且a,b满足(a-4)2+|b-4|=0,连接AB,∠OBA=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
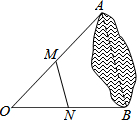 如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M,N,测得MN=39m,则A,B两点间的距离是78m.
如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M,N,测得MN=39m,则A,B两点间的距离是78m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com