练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若随机变量X～N（2，32），且P（X≤1）=P（X≥a），则（x+a）2（ax﹣ ）5展开式中x3项的系数是 ．

    【答案】1620
    【解析】解：随机变量X～N（2，32），均值是2， 且P（X≤1）=P（X≥a），
    ∴a=3；
    ∴（x+a）2（ax﹣ ）5=（x+3）2（3x﹣ ）5=（x2+6x+9） ；
    又 展开式的通项公式为
    Tr+1= （3x）5﹣r =（﹣1）r35﹣r ，
    令5﹣ =1，解得r= ，不合题意，舍去；
    令5﹣ =2，解得r=2，对应x2的系数为（﹣1）223 =270；
    令5﹣ =3，解得r= ，不合题意，舍去；
    ∴展开式中x3项的系数是6×270=1620．
    所以答案是：1620．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，2 ），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线第一次垂直时，点P的坐标为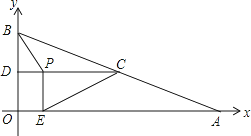

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知F1、F2分别为双曲线C： =1的左、右焦点，P为双曲线C右支上一点，且|PF1|=2|PF2|，则△PF1F2外接圆的面积为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且 =0． （Ⅰ）求角B的大小；
    （Ⅱ）若b= ，a+c=4，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代数学著作《九章算术》有如下问题：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米一斗五升．问，米几何？”如图是解决该问题的程序框图，执行该程序框图，若输出的S=1.5（单位：升），则输入k的值为（ ）
    A.4.5
    B.6
    C.7.5
    D.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，∠ADC=90°，AD∥BC，AB⊥AC，AB=AC= ，点E在AD上，且AE=2ED．
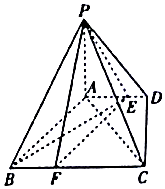
    （Ⅰ）已知点F在BC上，且CF=2FB，求证：平面PEF⊥平面PAC；
    （Ⅱ）当二面角A﹣PB﹣E的余弦值为多少时，直线PC与平面PAB所成的角为45°？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数 ，若将f（x）的图象向左平移 个单位后所得函数的图象关于原点对称，则φ=（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知四棱锥P﹣ABCD，底面ABCD为矩形，点E，F在侧棱PA，PB上且PE=2EA，PF=2FB，点M为四棱锥内任一点，则M在平面EFCD上方的概率是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1）所示，已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的，其中∠SAB=∠SDC=90°，且点A为线段SD的中点，AD=2DC=1，AB=SD，现将△SAB沿AB进行翻折，使得二面角S﹣AB﹣C的大小为90°，得到的图形如图（2）所示，连接SC，点E、F分别在线段SB、SC上．
    （1）证明：BD⊥AF；
    （2）若三棱锥B﹣AEC的体积是四棱锥S﹣ABCD体积的 ，求点E到平面ABCD的距离．

    查看答案和解析>>

    同步练习册答案