
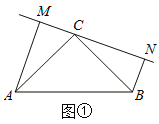
【题目】如图①:在△ABC中,∠ACB=90![]() ,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
(1)求证:MN=AM+BN.
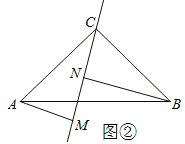
(2)如图②,若过点C在△ABC内作直线MN,AM⊥MN于点M,BN⊥MN于点N,则猜想AM、BN与MN之间有什么关系?请直接写出结论,并写出图②中的全等三角形.
【答案】(1)见解析;(2)MN=BN-AM (或AM=BN-MN或BN=AM+MN)
【解析】试题分析:
(1)由AM⊥MN于点M,BN⊥MN于点N可得∠AMC=∠BNC=∠ACB=90°,由此可得∠MAC+∠ACM=90°,∠ACM+∠BCN=90°,从而可得∠MAC=∠BCN,结合AC=BC,即可证得△ACM≌△CBN,即可得到MC=BN,AM=CN,结合MN=MC+CN可得MN=AM+BN;
(2)由题意和(1)同理可证△ACM≌△CBN,从而可得MN=BN-AM (或AM=BN-MN或BN=AM+MN).
试题解析:
(1)∵AM⊥MN, BN⊥MN,
∴∠AMC=∠CNB=∠ACB=90![]() ,
,
∴∠MAC+∠ACM=90![]() ,∠NCB+∠ACM=90
,∠NCB+∠ACM=90![]() ,
,
∴∠MAC=∠NCB,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,
∴△AMC≌△CNB(AAS),
∴AM=NC ,MC=BN,
∵MN=NC+MC,
∴MN=AM+BN,
(2)∵AM⊥MN, BN⊥MN,
∴∠AMC=∠CNB=∠ACB=90![]() ,
,
∴∠MAC+∠ACM=90![]() ,∠NCB+∠ACM=90
,∠NCB+∠ACM=90![]() ,
,
∴∠MAC=∠NCB,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,
∴△AMC≌△CNB(AAS),
∴AM=NC,MC=BN,
∵MN=MC-CN,
∴MN=BN-AM (或AM=BN-MN或BN=AM+MN).


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,(1)P是等腰三角形A BC底边BC上的一人动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R。请观察AR与AQ,它们有何关系?并证明你的猜想。

(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图15(2)中完成图 形,并给予证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分) “先学后教”课题组对学生参与小组合作的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.课题组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了______名学生;
(2)请将条形统计图补充完整;
(3)求出扇形统计图中,“主动质疑”所对应扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在半径为2的半圆O中,半径OA垂直于直径BC,点E与点F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合. 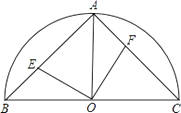
(1)求四边形AEOF的面积.
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式,求x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+6+62+63+64+65+66+67+68+69的值时,小林发现:从第二个加数起每一个加数都是前一个加数的6倍,于是她设:S=1+6+62+63+64+65+66+67+68+69①,然后在①式的两边都乘以6,得6S=6+62+63+64+65+66+67+68+69+610②,②-①得6S-S=610-1,即5S=610-1,所以S=![]() ,得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2016的值?你的答案是( )
,得出答案后,爱动脑筋的小林想:如果把“6”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2016的值?你的答案是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到![]() (0,1),
(0,1),![]() (1,1),
(1,1),![]() (1,0),
(1,0),![]() (2,0),…那么点
(2,0),…那么点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com