
【题目】如图,在菱形ABCD中,AB=4,线段AD的垂直平分线交AC于点N,△CND的周长是10,则AC的长为 . 
【答案】6
【解析】解:如图, 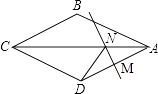
∵四边形ABCD是菱形,AB=4,
∴AB=CD=4,
∵MN垂直平分AD,
∴DN=AN,
∵△CND的周长是10,
∴CD+CN+DN=CD+CN+AN=CD+AC=10,
∴AC=6,
所以答案是:6.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
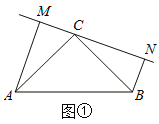
【题目】如图①:在△ABC中,∠ACB=90![]() ,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
,△ABC是等腰直角三角形,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
(1)求证:MN=AM+BN.
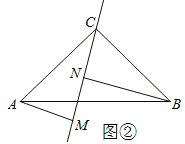
(2)如图②,若过点C在△ABC内作直线MN,AM⊥MN于点M,BN⊥MN于点N,则猜想AM、BN与MN之间有什么关系?请直接写出结论,并写出图②中的全等三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商行计划购进A、B两种水果共200箱,这两种水果的进价、售价如下表所示:
价格 | 进价(元/箱) | 售价(元/箱) |
A | 60 | 70 |
B | 40 | 55 |
(1)若该商行进贷款为1万元,则两种水果各购进多少箱?
(2)若商行规定A种水果进货箱数不低于B种水果进货箱数的 ![]() ,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?
,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]()
(1)请直接写出方程![]() 的所有正整数解
的所有正整数解
(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S﹣S=22014﹣1
即S=22014﹣1
即1+2+22+23+24+…+22013=22014﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(请在括号里注明重要的推理依据)
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜抽样调查的是( )
A.了解某班学生的身高情况
B.选出某校短跑最快的学生参加全市比赛
C.了解全班同学每周体育锻炼的时间
D.调查某批次汽车的抗撞击能力
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com