
【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF 
(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形.
【答案】
(1)证明:连接DB,CF,
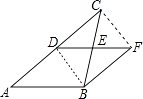
∵DE是△ABC的中位线,
∴CE=BE,
∵EF=ED,
∴四边形CDBF是平行四边形,
∴CD=BF
(2)证明:∵四边形CDBF是平行四边形,
∴CD∥FB,
∴AD∥BF,
∵DE是△ABC的中位线,
∴DE∥AB,
∴DF∥AB,
∴四边形ABFD是平行四边形
【解析】(1)连接DB,CF,利用对角线互相平分的四边形是平行四边形可得四边形CDBF是平行四边形,进而可得CD=BF;(2)由(1)可得CD∥FB,再利用三角形中位线定理可得DF∥AB,根据两组对边分别平行的四边形是平行四边形可得结论.
【考点精析】利用三角形中位线定理和平行四边形的判定对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.对角线相等的四边形是菱形B.有一组邻边相等的平行四边形是菱形
C.四条边相等的四边形是矩形D.对角线互相垂直的平行四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假就要来了,小明为自己制定了慢跑锻炼计划,某日小明从家出发沿解放路慢跑,已知他离家的距离s(千米)与时间t(分钟)之间的关系如图所示,请根据图象直接回答下列问题: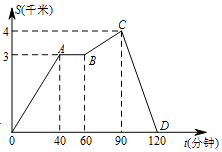
(1)小明离开家的最远距离是多少千米,他在120分钟内共跑了多少千米;
(2)小明在这次慢跑过程中,停留所用的时间为多少分钟;
(3)小明在这段时间内慢跑的最快速度是每小时多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
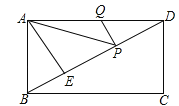
【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
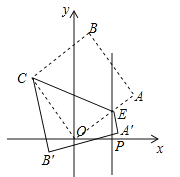
【题目】如图,在平面直角坐标系中,坐标原点O是正方形OABC的一个顶点,已知点B坐标为(1,7),过点P(a,0)(a>0)作PE⊥x轴,与边OA交于点E(异于点O、A),将四边形ABCE沿CE翻折,点A′、B′分别是点A、B的对应点,若点A′恰好落在直线PE上,则a的值等于( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com