
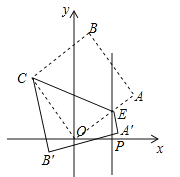
【题目】如图,在平面直角坐标系中,坐标原点O是正方形OABC的一个顶点,已知点B坐标为(1,7),过点P(a,0)(a>0)作PE⊥x轴,与边OA交于点E(异于点O、A),将四边形ABCE沿CE翻折,点A′、B′分别是点A、B的对应点,若点A′恰好落在直线PE上,则a的值等于( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
【答案】C.
【解析】当点A′恰好落在直线PE上,如图所示,连接OB、AC,交于点D,过点C作CF∥A′B′,交PE于点F,交y轴于点G,则CF⊥y轴,∵四边形OABC是正方形,∴OD=BD,OB⊥AC,∵O(0,0),B(1,7),∴D(![]() ,
,![]() ),由勾股定理得:OB=
),由勾股定理得:OB=![]() =
=![]() =
=![]() ,设直线OB的解析式为:y=kx,把B(1,7)代入得:k=7,∴直线OB的解析式为:y=7x,∴设直线AC的解析式为:
,设直线OB的解析式为:y=kx,把B(1,7)代入得:k=7,∴直线OB的解析式为:y=7x,∴设直线AC的解析式为:![]() ,把D(
,把D(![]() ,
,![]() )代入得:
)代入得:![]() ,c=
,c=![]() ,∴直线AC的解析式为:
,∴直线AC的解析式为:![]() ,设C(x,
,设C(x,![]() ),在Rt△OBC中,cos∠BOC=
),在Rt△OBC中,cos∠BOC=![]() ,∴OC=cos45°OB=
,∴OC=cos45°OB=![]() =5,∴正方形OABC的边长为5,由翻折得:A′B′=AB=5,在Rt△OCG中,
=5,∴正方形OABC的边长为5,由翻折得:A′B′=AB=5,在Rt△OCG中,![]() ,∴
,∴![]() ,解得:x1=﹣3,x2=4(舍),∴CG=3,∵CF=A′B′=5,∴FG=CF﹣CG=5﹣3=2,∴P(2,0),即a=2,故选C.
,解得:x1=﹣3,x2=4(舍),∴CG=3,∵CF=A′B′=5,∴FG=CF﹣CG=5﹣3=2,∴P(2,0),即a=2,故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
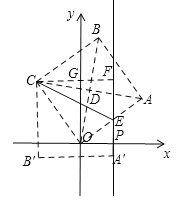
【题目】((2016江苏省苏州市中考预测)囧(读jiǒng)原是一个今已罕用的文字,由于囧字外观貌似失意的表情,近年在网络间成为一个流行的表情符号.如图是一个近似“囧”的图形,若已知四边形ABCD是一个边长为2a的正方形,P、M、N分别是边AD、AB、CD的中点,E、H分别是PM、PN的中点,则正方形EFGH的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的高,AM是△ABC外角∠CAE的平分线. 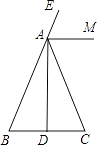
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.四个角相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线垂直的四边形是菱形
D.对角线垂直的平行四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题“三角形中至少有一个内角小于或等于60°”时,首先应该假设这个三角形中( ).
A. 每一个内角都大于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 有一个内角小于60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图四边形AOBC为正方形,点C的坐标为(4 ![]() ,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
,0),动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动,同时点Q沿着折线OBCA的方向匀速运动,速度是2个单位长度每秒,运动时间为t秒,当他们相遇时同时停止运动.
(1)点A的坐标是正方形AOBC的面积是 .
(2)将正方形绕点O顺时针旋转45°,求旋转后的正方形与原正方形的重叠部分的面积.
(3)运动时间t为多少秒时,以A、P、B、Q四点为顶点的四边形为平行四边形?
(4)是否存在这样的t值,使△OPQ成为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com