
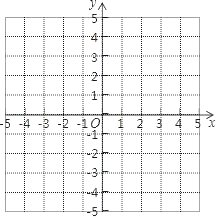
【题目】在下面所给的平面直角坐标系中,解答下列问题
(1)描出点A(﹣2,0),B(2,﹣1),C(3,3),并用线段依次连接起来.
(2)将三角形ABC向左平移2个单位长度,再向下平移3个单位长度,得到三角形A′B′C′.
(3)写出三角形A′B′C′各个顶点的坐标.
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)工厂补充10名新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置,则补充新工人后每天能配套生产多少产品?
(3)为了在规定期限内完成总任务,请问至少需要补充多少名(2)中的新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于![]() cm2?
cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
氢动力汽车是一种真正实现零排放的交通工具,排放出的是纯净水,其具有无污染,零排放,储量丰富等优势,因此,氢动力汽车是传统汽车最理想的替代方案.某实验团队进行氢动力汽车实验,在一条笔直的公路上有![]() ,
,![]() 两地,小张驾驶氢动力汽车从
两地,小张驾驶氢动力汽车从![]() 地去
地去![]() 地然后立即原路返回到
地然后立即原路返回到![]() 地,小陈驾驶观察车从
地,小陈驾驶观察车从![]() 地驶向
地驶向![]() 地.如图是氢动力汽车、观察车离
地.如图是氢动力汽车、观察车离![]() 地的距离
地的距离![]() 和行驶时间
和行驶时间![]() 之间的函数图象,请根据图象回答下列问题:
之间的函数图象,请根据图象回答下列问题:
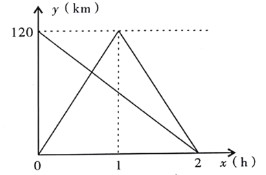
(1)![]() ,
,![]() 两地的距离是______
两地的距离是______![]() ,小陈驾驶观察车行驶的速度是______
,小陈驾驶观察车行驶的速度是______![]() ;
;
(2)当小张驾驶氢动力汽车从![]() 地原路返回
地原路返回![]() 地时,有一段时间小陈驾驶的观察车与氢动力汽车之间的距离不超过30千米,请探究此时行驶时间
地时,有一段时间小陈驾驶的观察车与氢动力汽车之间的距离不超过30千米,请探究此时行驶时间![]() 在哪一范围内?
在哪一范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() .
.
(感知)如图1,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .易证
.易证![]() .(不需要证明)
.(不需要证明)

(探究)如图2,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)连接![]() .若
.若![]() ,则
,则![]() 的长为___________.
的长为___________.

(应用)如图3,取![]() 的中点
的中点![]() ,连接
,连接![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,则四边形
,则四边形![]() 的面积为______.
的面积为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com