
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
科目:初中数学 来源: 题型:
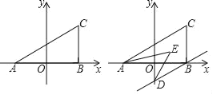
【题目】如图,在平面坐标系中,A(a,0),B(b,0),C(x,y)且满足(a+b)2+|a﹣b﹣4|=0,y=![]() +2.
+2.
(1)求三角形ABC的面积;
(2)若过B作BD∥AC交y轴于D,且AE、DE平分∠CAB、∠ODB,如图,求∠AED的度数;
(3)在y轴上是否存在点P,①使得△ABC和△ACP的面积相等,若存在,求出P点的坐标:若不存在,请说明理由;②若△ACP的面积是△ABC面积的2018倍成立,直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
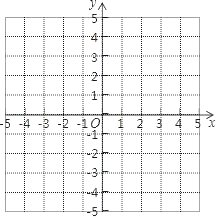
【题目】在下面所给的平面直角坐标系中,解答下列问题
(1)描出点A(﹣2,0),B(2,﹣1),C(3,3),并用线段依次连接起来.
(2)将三角形ABC向左平移2个单位长度,再向下平移3个单位长度,得到三角形A′B′C′.
(3)写出三角形A′B′C′各个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )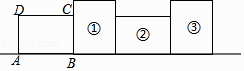
A.2017π
B.2034π
C.3024π
D.3026π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第1次用600元购进2B铅笔若干支,第2次用800元又购进该款铅笔,但这次每支的进价是第1次进价的八折,且购进数量比第1次多了100支.
(1)求第1次每支2B铅笔的进价;
(2)若要求这两次购进的2B铅笔按同一价格全部销售完毕后获利不低于600元,问每支2B铅笔的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证. (以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据该图完成这个推论的证明过程.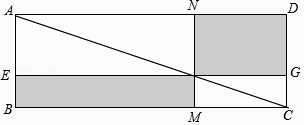
证明:S矩形NFGD=S△ADC﹣(S△ANF+S△FGC),S矩形EBMF=S△ABC﹣(+).
易知,S△ADC=S△ABC , = , = .
可得S矩形NFGD=S矩形EBMF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com