
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证. (以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据该图完成这个推论的证明过程.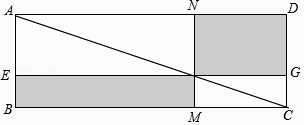
证明:S矩形NFGD=S△ADC﹣(S△ANF+S△FGC),S矩形EBMF=S△ABC﹣(+).
易知,S△ADC=S△ABC , = , = .
可得S矩形NFGD=S矩形EBMF .
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠C=40°,P,Q分别在BC,CA上,AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表,去年销售总额为8000元,今年A型智能手表的售价每只比去年降了60元,若售出的数量与去年相同,销售总额将比去年减少25%.
(1)请问今年A型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价与销售价格如下表,若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
A型智能手表 | B型智能手表 | |
进价 | 130元/只 | 150元/只 |
售价 | 今年的售价 | 230元/只 |
查看答案和解析>>
科目:初中数学 来源: 题型:
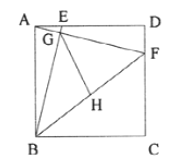
【题目】已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() .
.
(感知)如图1,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .易证
.易证![]() .(不需要证明)
.(不需要证明)

(探究)如图2,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)连接![]() .若
.若![]() ,则
,则![]() 的长为___________.
的长为___________.

(应用)如图3,取![]() 的中点
的中点![]() ,连接
,连接![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,则四边形
,则四边形![]() 的面积为______.
的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定组织学生开展校外拓展活动,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲乙两种大客车,它们的载客量和租金如下表所示.学校计划此次拓展活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
客车 | 甲种 | 乙种 |
载客量/(人/辆) | 30 | 42 |
租 金/(元/辆) | 300 | 400 |
(1)参加此次拓展活动的老师有 人,参加此次拓展活动的学生有 人;
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆.
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com