
【题目】某校决定组织学生开展校外拓展活动,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲乙两种大客车,它们的载客量和租金如下表所示.学校计划此次拓展活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
客车 | 甲种 | 乙种 |
载客量/(人/辆) | 30 | 42 |
租 金/(元/辆) | 300 | 400 |
(1)参加此次拓展活动的老师有 人,参加此次拓展活动的学生有 人;
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆.
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
【答案】(1)16,284;(2)8;(3)共有3种租车方案:方案一:租用甲种客车3辆,乙种客车5辆,租车费用为2900元;方案二:租用甲种客车2辆,乙种客车6辆,租车费用为3000元;方案三:租用甲种客车1辆,乙种客车7辆,租车费用为3100元;最节省费用的租车方案是:租用甲种客车3辆,乙种客车5辆.
【解析】
(1)设老师有x名,学生有y名,根据若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生列出方程组 ,求解即可;
(2)每辆客车上至少要有2名老师,而老师的总数量是16 ,故汽车总数不能大于8辆;老师和学生一共300人 ,要保证所有师生都有车坐,故汽车总数不能小于![]() 辆,综合起来可知汽车总数为8辆;
辆,综合起来可知汽车总数为8辆;
(3)设租用x辆乙种客车,则甲种客车数为: (8-x)辆,由租车总费用不超过3100元,为使300名师生都有座,列出不等式组,求解得出其整数解即可得出答案.
(1)解:设老师有x名,学生有y名,
依题意,列方程组为
![]()
解得:
![]()
答:老师有16名,学生有284名.
(2)因为每辆客车上至少要有2名老师,
所以汽车总数不能大于8辆;
又要保证300名师生有车坐,汽车总数不能小于![]() ( 取整为8 )辆,
( 取整为8 )辆,
综合起来可知汽车总数为8辆,
故答案为: 8;
(3)解:设租用x辆乙种客车,则甲种客车数为: (8-x)辆,
因为车总费用不超过3100元,
所以400x+300(8-x)≤3100 ,
解得:x≤7,
为使300名师生都有座,
所以42x+30(8-x)≥300 ,
解得:x≥5,
所以5≤x≤7 ( x为整数),
所以共有3种租车方案:
方案一:租用甲种客车3辆,乙种客车5辆,租车费用为2900元;
方案二:租用甲种客车2辆,乙种客车6辆,租车费用为3000元;
方案三:租用甲种客车1辆,乙种客车7辆,租车费用为3100元;
故最节省费用的租车方案是:租用甲种客车3辆,乙种客车5辆.


科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证. (以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据该图完成这个推论的证明过程.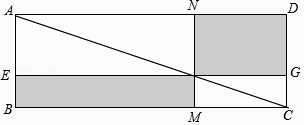
证明:S矩形NFGD=S△ADC﹣(S△ANF+S△FGC),S矩形EBMF=S△ABC﹣(+).
易知,S△ADC=S△ABC , = , = .
可得S矩形NFGD=S矩形EBMF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿AB方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形?
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转得到
按顺时针方向旋转得到![]() ,使
,使![]() 所在直线经过点
所在直线经过点![]() ,则直线
,则直线![]() 的解析式为__________.
的解析式为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD(AB<AD).
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹;
①以点A为圆心,以AD的长为半径画弧交边BC于点E,连接AE;
②作∠DAE的平分线交CD于点F;
③连接EF;
(2)在(1)作出的图形中,若AB=8,AD=10,则tan∠FEC的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在边AB、CB上,CD=DE,∠CDB=∠DEC,过点C作CF⊥DE于点F,交AB于点G,
(1)求证:△ACD≌△BDE;
(2)求证:△CDG为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(﹣2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com