
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿AB方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形?
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.

【答案】
【1】(1)出发2秒后,BP=6,BQ=4,PQ=![]() ;
;
【2】(2)设时间为t,列方程得
2t=8-1×t,
解得t=![]() ;
;
【3】(3)根据勾股定理可知AC=10cm,即三角形的周长为24cm,则有BP+BQ=12,
设时间为t,列方程得]
2t+(8-1×t)=12,
解得t=4,
当t=4时,点Q运动的路程是4×2=8>6,
所以不能够. ………………………………………………………(4分)
【解析】
(1)我们求出BP、BQ的长,用勾股定理解决即可.
(2)△PQB形成等腰三角形,即BP=BQ,我们可设时间为t,列出方程2t=8-1×t,解方程即得结果.
(3)直线PQ把原三角形周长分成相等的两部分,根据勾股定理可知AC=10cm,即三角形的周长为24cm,则有BP+BQ=12,即![]() 解方程即可
解方程即可
解:(1)出发2秒后,BP=6,BQ=4,PQ=![]() ;
;
(2)设时间为t,列方程得
2t=8-1×t,
解得t=![]() ;
;
(3)根据勾股定理可知AC=10cm,即三角形的周长为24cm,则有BP+BQ=12,
设时间为t,列方程得
![]()
解得t=4,
当t=4时,点Q运动的路程是4×2=8>6,
所以不能够.
本题重点考查了利用勾股定理解决问题的能力,综合性较强.


科目:初中数学 来源: 题型:
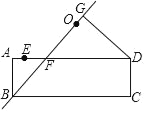
【题目】如图,矩形ABCD中,AB=3,AD=9,点E在边AD上,AE=1,过E、D两点的圆的圆心O在边AD的上方,直线BO交AD于点F,作DG⊥BO,垂足为G.当△ABF与△DFG全等时,⊙O的半径为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.

(1)请写出图中全等三角形(不再添加辅助线).
(2)求证:△ABE≌△CDF;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:已知方程a2![]() 2a
2a![]() 1=0,1
1=0,1![]() 2b
2b![]() b2=0且ab≠1,求
b2=0且ab≠1,求![]() 的值.
的值.
解:由a2![]() 2a
2a![]() 1=0及1
1=0及1![]() 2b
2b![]() b2=0,
b2=0,
可知a≠0,b≠0,
又∵ab≠1,![]() .
.
1![]() 2b
2b![]() b2=0可变形为
b2=0可变形为
![]() ,
,
根据a2![]() 2a
2a![]() 1=0和
1=0和![]() 的特征.
的特征.
![]() 、
、![]() 是方程x2
是方程x2![]() 2x
2x![]() 1=0的两个不相等的实数根,
1=0的两个不相等的实数根,
则![]() ,即
,即![]() .
.
根据阅读材料所提供的方法,完成下面的解答.
已知:3m2![]() 7m
7m![]() 2=0,2n2+7n
2=0,2n2+7n![]() 3=0且mn≠1,求
3=0且mn≠1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE和CE分别为△ABC的内角平分线和外角平分线,BE⊥AC于点H,CF平分∠ACB交BE于点F连接AE.则下列结论:①∠ECF=90°;②AE=CE;③![]() ;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的个数为( )
;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的个数为( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=45°,BC=2,D是线段BC上的一个动点,点D是关于直线AB、AC的对称点分别为M、N,则线段MN长的最小值是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com