
【题目】如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.
求证:DE=BF.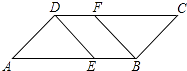
【答案】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=CF.
∴BE=FD,BE∥FD,
∴四边形EBFD是平行四边形,
∴DE=BF
【解析】方法一:根据平行四边形的性质得出AB平行且等于CD,由AE=CF得出BE=FD,BE∥FD,即可证得四边形EBFD是平行四边形,根据平行四边形的性质即可证得结论。
方法二:由已知平行四边形得出对角相等,对边相等,再证明△ADE≌△CBF,即可求得DE=CF.
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图所示的表格是某次篮球联赛部分球队的积分表,则下列说法不正确的是( )
队名 | 比赛场数 | 胜场 | 负场 | 积分 |
前进 | 14 | 10 | 4 | 24 |
光明 | 14 | 9 | 5 | 23 |
远大 | 14 | 7 | a | 21 |
卫星 | 14 | 4 | 10 | b |
钢铁 | 14 | 0 | 14 | 14 |
… | … | … | … | … |
A.负一场积1分,胜一场积2分B.卫星队总积分b=18
C.远大队负场数a=7D.某队的胜场总积分可以等于它的负场总积分
查看答案和解析>>
科目:初中数学 来源: 题型:
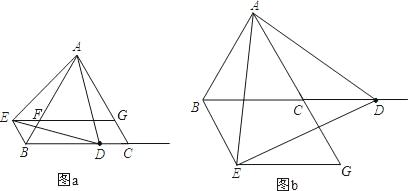
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
(1)如图(a)所示,当点D在线段BC上时.
①求证:△AEB≌△ADC;
②探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图(b)所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立;
(3)在(2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)经过A(﹣3,0)、B(1,0)两点,与y轴交于点C,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线PE,垂足点为E,连接AE.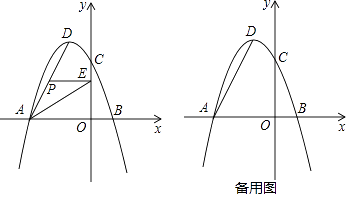
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线PF,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实验课上,王老师让大家用矩形纸片折出菱形.小华同学的操作步骤是:
(1)如图①,将矩形ABCD沿着对角线BD折叠;
(2)如图②,将图①中的△A’BF沿BF折叠得到△A’’BF;
(3)如图③,将图②中的△CDF沿DF折叠得到△C’DF;
(4)将图③展开得到图④,其中BD、BE、DF为折叠过程中产生的折痕.

试解答下列问题:
(1)证明图④中的四边形BEDF为菱形;
(2)在图④中,若BC=8,CD=4,求菱形BEDF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为贯彻落实云南省教育厅提出的“三生教育”,在母亲节来临之际,某校团委组织了以“珍爱生命,学会生存,感恩父母”为主题的教育活动,在学校随机调查了50名同学平均每周在家做家务的时间,统计并制作了如下的频数分布和扇形统计图:
组别 | 做家务的时间 | 频数 | 频率 |
A | 1≤t<2 | 3 | 0.06 |
B | 2≤t<4 | 20 | 0.40 |
C | 4≤t<6 | A | 0.30 |
D | 6≤t<8 | 8 | B |
E | t≥8 | 4 | 0.08 |
根据上述信息回答下列问题: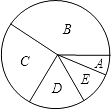
(1)a= , b=;
(2)在扇形统计图中,B组所占圆心角的度数为;
(3)全校共有2000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京某中学为了迎接世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:

请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整:
(3)若测试成绩不低于90分的同学可以获得世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿AB方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形?
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com