
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�������y=ax2+bx+3��a��0������A����3��0����B��1��0�����㣬��y�ύ�ڵ�C���䶥��ΪD������AD����P���߶�AD��һ�����㣨����A��D�غϣ�������P��y��Ĵ���PE�������ΪE������AE��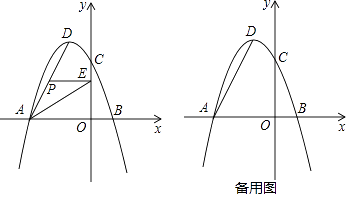
��1���������ߵĺ�������ʽ����д������D�����ꣻ
��2�����P�������Ϊ��x��y������PAE�����ΪS����S��x֮��ĺ�����ϵʽ��ֱ��д���Ա���x��ȡֵ��Χ�������S�����ֵ��
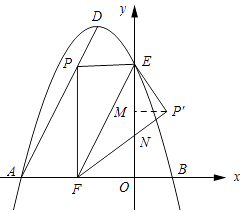
��3���ڣ�2���������£���Sȡ�����ֵʱ������P��x��Ĵ���PF������ΪF������EF���ѡ�PEF��ֱ��EF�۵�����P�Ķ�Ӧ��Ϊ��P�䣬���P������꣬���ж�P���Ƿ��ڸ��������ϣ�
���𰸡�
��1���⣺����A�͵�B���������ã� ![]() ��
��
��ã�a=1��b=��2��
�������ߵĽ���ʽΪy=��x2��2x+3��
��y=��x2��2x+3=����x+1��2+4��
�������ߵĶ�������ΪDΪ����1��4��
��2���⣺��AD�Ľ���ʽΪy=kx+b������A�͵�D���������ã� ![]() ��
��
��ã�k=2��b=6��
��P��AD�ϣ�
��P��x��2x+6����
��S= ![]() PEyP=
PEyP= ![]() ����x����2x+6��=��x2��3x����3��x����1����
����x����2x+6��=��x2��3x����3��x����1����
�൱x=�� ![]() =��
=�� ![]() ʱ��Sȡֵ���ֵ
ʱ��Sȡֵ���ֵ ![]()
��3���⣺��ͼ1��ʾ����P��F��y�ύ���N������P����P��M��y�����M��
�ߵ�x=�� ![]() ʱ��Sȡֵ���ֵ��
ʱ��Sȡֵ���ֵ��
��P���� ![]() ��3����
��3����
�ɷ��۵����ʿ�֪����PFE=��P��FE��PF=P��F=3��PE=P��E= ![]() ��
��
��PF��y�ᣮ
���PFE=��FEN��
��EN=FN��
��EN=m����FN=m��P��N=3��m��
����Rt��P��EN��P��N2+P��E2=EN2��
�ࣨ3��m��2+�� ![]() ��2=m2����ã�m=
��2=m2����ã�m= ![]() ��
��
��S��P��EN= ![]() P��NP��E=
P��NP��E= ![]() ENP��M��
ENP��M��
��P��M= ![]() ��
��
����Rt��EMP����EM= ![]() =
= ![]() ��
��
��OM=EO��EM= ![]() ��
��
��P�䣨 ![]() ��
�� ![]() ����
����
��x= ![]() ���������ߵĽ���ʽ�ã�y=
���������ߵĽ���ʽ�ã�y= ![]() ��
�� ![]() ��
��
���P�䲻�ڸ���������
����������1���ô���ϵ������A��B����������뺯������ʽ������⣬�����䷽������붥�㹫ʽ����������ꡣ
��2��Ҫ���PAE�����������PE��y�ᣬ��PAE�����=![]() PE
PE![]() PE���ϵĸߣ���˾͵����ֱ��AD�ĺ�������ʽ�����ݵ�P��ֱ��AD�ϣ������ú�x�Ĵ���ʽ���PE��PE���ϵĸߣ�����д��s��x �ĺ�����ϵʽ��������������꼴����ý����
PE���ϵĸߣ���˾͵����ֱ��AD�ĺ�������ʽ�����ݵ�P��ֱ��AD�ϣ������ú�x�Ĵ���ʽ���PE��PE���ϵĸߣ�����д��s��x �ĺ�����ϵʽ��������������꼴����ý����
��3��Ҫ���P������꣬����P����P��M��y�����M���ɣ�2���ó���P�����꣬�����۵������ʣ�����֤�á�PFE=��P��FE��PF=P��F��PE=P��E����֤��EN=FN����Rt��P��EN�У����ù��ɶ������EN�ij����ٸ���ֱ�������ε����������ֱ�DZ���һ�����б�߳���б���ϵĸߣ����P��M�ij�����Rt��EMP�������EM�ij����������OM�ij����Ϳ���д����P������꣬�ٽ���P��ĺ�������뺯������ʽ�Ϳ�֪����P���Ƿ��ڴ��������ϡ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
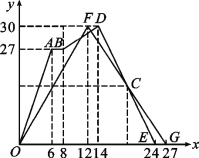
����Ŀ���ס�������ͬѧ�桰���˱�������������ÿ������ͬѧ�ñ�������������涨��·�̣���;�������ʱ����ص����������ܣ���ʱ����ʤ�������������λͬѧ������������λͬѧ˳�����꣮�������ͬѧ�������ľ�����y��ʾ����λ���ף�����ʱ����x��ʾ����λ���룮����ͬѧ����������ͼ���ʾ���£�
(1)����һ�� �ı����������
(2)�߶� ��ʾ������λͬѧ�ڱ�����;�������� �룻
(3)����ͬѧ�����յ����� �룬����ͬѧ�����յ����� �룬��ʤ���� ��ͬѧ��
(4)��ֱ��д��C�����꣬��˵����C��ʵ�����壮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
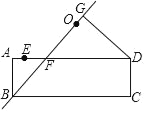
����Ŀ����ͼ������ABCD�У�AB��3��AD��9����E�ڱ�AD�ϣ�AE��1����E��D�����Բ��Բ��O�ڱ�AD���Ϸ���ֱ��BO��AD�ڵ�F����DG��BO������ΪG������ABF���DFGȫ��ʱ����O�İ뾶Ϊ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������λ�ڳ������˵�A��B����ľ��룮��������ֱ��ABƽ�еĵ�·EF���ߣ������ߵ���C������á�ACF=45�㣬����ǰ����100����D������á�BDF=60�㣮��ֱ��AB��EF֮��ľ���Ϊ60�ף���A��B����ľ��룮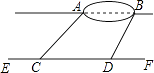
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���BAC��90������D��BC��һ�㣬����ABD��AD���ۺ�õ���AED����AE��BC�ڵ�F��


(1)��ͼ�٣���AE��BCʱ��д��ͼ���������B��ȵĽǣ��� ���������C��ȵĽǣ��� �� ��
(2)����C����B��50������BAD��x��(0��x��45) ��
�� ���B�Ķ�����
���Ƿ����������x��ֵ��ʹ�á�DEF������������ȣ������ڣ�����x��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��

��1����֤��OE=OF��
��2����CE=12��CF=5����OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���֪��E��AB�ϣ���F��CD�ϣ���AE=CF��
��֤��DE=BF��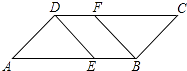
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�εĸ���Ϊ�� �� 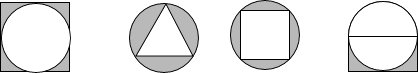
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BE��CE�ֱ�Ϊ��ABC���ڽ�ƽ���ߺ����ƽ���ߣ�BE��AC�ڵ�H��CFƽ�֡�ACB��BE�ڵ�F����AE�������н��ۣ��١�ECF=90������AE=CE����![]() ���ܡ�BAC=2��BEC���ݡ�AEH=��BCF����ȷ�ĸ���Ϊ�� ��
���ܡ�BAC=2��BEC���ݡ�AEH=��BCF����ȷ�ĸ���Ϊ�� ��

A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com