
【题目】如图,已知矩形ABCD(AB<AD).
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹;
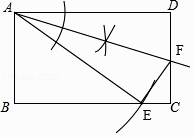
①以点A为圆心,以AD的长为半径画弧交边BC于点E,连接AE;
②作∠DAE的平分线交CD于点F;
③连接EF;
(2)在(1)作出的图形中,若AB=8,AD=10,则tan∠FEC的值为 .
【答案】
(1)
解:如图所示;
(2)![]()
【解析】解:(1.)如图所示;
(2.)由(1)知AE=AD=10、∠DAF=∠EAF,
∵AB=8,
∴BE= ![]() =6,
=6,
在△DAF和△EAF中,
∵ 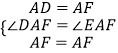 ,
,
∴△DAF≌△EAF(SAS),
∴∠D=∠AEF=90°,
∴∠BEA+∠FEC=90°,
又∵∠BEA+∠BAE=90°,
∴∠FEC=∠BAE,
∴tan∠FEC=tan∠BAE= ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
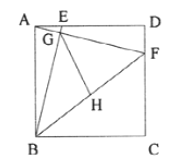
【题目】已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G. 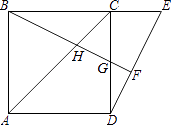
(1)求证:BG=DE;
(2)若点G为CD的中点,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分20分,题b、题c满分均为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,在这个班的平均成绩是__分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定组织学生开展校外拓展活动,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲乙两种大客车,它们的载客量和租金如下表所示.学校计划此次拓展活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
客车 | 甲种 | 乙种 |
载客量/(人/辆) | 30 | 42 |
租 金/(元/辆) | 300 | 400 |
(1)参加此次拓展活动的老师有 人,参加此次拓展活动的学生有 人;
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆.
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.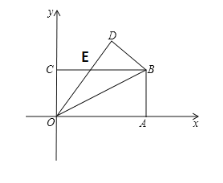
(1)求点E的坐标;
(2)点M是OB上任意一点,点N是OA上任意一点,是否存在点M、N,使得AM+MN最小?若存在,求出其最小值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有![]() 三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时的频数 公交车用时线路 |
|
|
|
| 合计 |
| 59 | 151 | 166 | 124 | 500 |
| 50 | 50 | 122 | 278 | 500 |
| 45 | 265 | 160 | 30 | 500 |
早高峰期间,乘坐_________(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD、AE分别是Rt△ABC的高和中线,AB=9cm,AC=12cm,BC=15cm,试求:
(1)AD的长度;
(2)△ACE和△ABE的周长的差.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com