练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在方程ax=12（a是正整数）中，x是未知数，a是用字母表示的已知数。于是，在项ax中，字母a是_____________，我们把a叫做_____________。这个方程是含有系数的_____________。在方程中，是未知数，b和s是用字母表示的已知数。同样地，字母b是______________字母s也叫做__________________，这个方程是含有系数的_____________。

    【答案】项ax的系数; 字母系数; 一元一次方程; 的系数; 常数; 一元二次方程.

    【解析】

    当方程中的系数用字母表示时，这个方程叫含字母系数的方程.不含求知数的字母项也叫常数.

    解：在方程ax=12（a是正整数）中，x是未知数，a是用字母表示的已知数.于是，在项ax中，字母a是项ax的系数，我们把a叫做字母系数.这个方程是含有系数的一元一次方程.在方程中，是未知数，b和s是用字母表示的已知数.同样地，字母b是的系数，字母s也叫做__常数_，这个方程是含有系数的一元二次方程.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

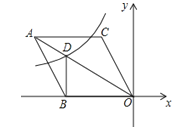
    【题目】如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC=60°，顶点C的坐标为（m，），反比例函数的图像与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是（　　）

    A. B. － C. D. －

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在数轴上A点表示数，B点表示数，、满足||+||=0；

    （1）点A表示的数为_____；点B表示的数为_____；

    （2）若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为t（秒），

    ①当t=1时，甲小球到原点的距离=_____；乙小球到原点的距离=_____.

    当t=3时，甲小球到原点的距离=_____；乙小球到原点的距离=_____.

    ②试探究：甲，乙两小球到原点的距离可能相等吗？若不能，请说明理由．若能，请直接写出甲，乙两小球到原点的距离相等时经历的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

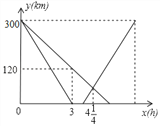
    【题目】某客运公司的特快巴士与普通巴士同时从甲地出发，以各自的速度匀速向乙地行驶，普通巴士到达乙地后停止，特快巴士到达乙地停留45分钟后，按原路以另一速度匀速返回甲地，已知两辆巴士分别距乙地的路程y（千米）与行驶时间x（小时）之间的函数图象如图所示．求普通巴士到达乙地时，特快巴士与甲地之间的距离为_____千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，坡AB的坡比为1：2.4，坡长AB=130米，坡AB的高为BT．在坡AB的正面有一栋建筑物CH，点H、A、T在同一条地平线MN上．

    （1）试问坡AB的高BT为多少米？

    （2）若某人在坡AB的坡脚A处和中点D处，观测到建筑物顶部C处的仰角分别为60°和30°，试求建筑物的高度CH．（精确到米， ≈1.73， ≈1.41）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂一个车间工人计划一周平均每天生产零件300个，实际每天生产量与计划每天生产量相比有误差.如表是这个车间工人在某一周每天的零件生产情况，超计划生产量为正、不足计划生产量为负.(单位：个)

    时间

    周一

    周二

    周三

    周四

    周五

    周六

    周日

    误差

    +10

    －15

    －6

    +12

    －10

    +18

    －11

    (1)生产零件数量最少的一天比最多的一天少生产______个零件；

    (2)若生产一个零件可得利润5元，则这个车间的工人在这一周为工厂一共带来了多少利润？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

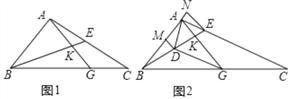
    【题目】如图1，已知△ABC中，∠ABC=45°，点E为AC上的一点，连接BE，在BC上找一点G，使得AG=AB，AG交BE于K．

    （1）若∠ABE=30°，且∠EBC=∠GAC，BK=4，求AC的长度．

    （2）如图2，过点A作DA⊥AE交BE于点D，过D、E分别向AB所在的直线作垂线，垂足分别为点M、N，且NE=AM，若D为BE的中点，证明： DG=2AG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一根长80厘米的弹簧，一端固定，如果另一端挂上物体，那么在正常情况下物体的质量每增加1千克可使弹簧增长2厘米。

    （1）正常情况下，当挂着千克的物体时，弹簧的长度是多少厘米？

    （2）正常情况下，当挂物体的质量为6千克时，弹簧的长度是多少厘米？

    （3）正常情况下，当弹簧的长度是120厘米时，所挂物体的质量是多少千克？

    （4）如果弹簧的长度超过了150厘米时，弹簧就失去弹性，问此弹簧能否挂质量为40千克的物体？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

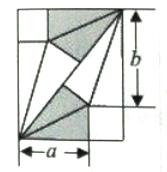
    【题目】我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理，如图所示的长方形由两个这样的图形拼成，若，，则该长方形的面积为__________.

    查看答案和解析>>

    同步练习册答案