
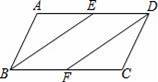
如图,在▱ABCD中,点E、F是AD、BC的中点,连接BE、DF.
(1)求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,试求线段DE的长.

【考点】平行四边形的判定与性质.
【分析】(1)由四边形ABCD是平行四边形,可得AD∥BC,AD=BC,又由点E、F分别是▱ABCD边AD、BC的中点,可得DE=BF,证得四边形BFDE是平行四边形,即可证得结论.
(2)由平行线的性质和角平分线得出∠ABE=∠AEB,证出AE=AB=6cm,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是▱ABCD边AD、BC的中点,
∴DE=
 AD,BF=
AD,BF=
 BC,
BC,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE=DF.
(2)解:∵AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=6cm,
∴DE=AD﹣AE=10cm﹣6cm=4cm.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
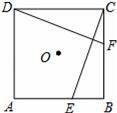
如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为 °.

查看答案和解析>>
科目:初中数学 来源: 题型:
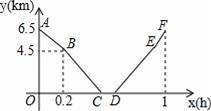
从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为 km/h,他在乙地休息了 h.
(2)分别求线段AB、EF所对应的函数关系式.
(3)从甲地到乙地经过丙地,如果小明两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的路程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com