
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,回答下列问题:
![]()
![]()
![]()
(1)试猜想:1+3+5+7+9+…+2015+2017+2019的和是多少?
(2)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少?
(3)计算:103+105+107+…+2017+2019.
查看答案和解析>>
科目:初中数学 来源: 题型:
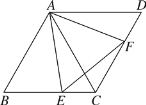
【题目】如图,△ABC和△ACD均为等边三角形,E是BC上的一个动点,F是CD上的一个动点,且∠EAF=60°.
(1)请判断△AEF的形状,并说明理由;
(2)当AB=4时,求△AEF面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
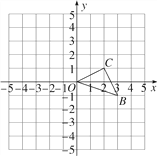
【题目】如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心,在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)如果△OBC内部一点M的坐标为(x,y),写出B,C,M的对应点B′,C′,M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com