

分析 (1)先用非负性求出a,b,从而确定出直线BC的解析式,进而求出直线AH解析式,即可;
(2)先求出OG解析式,进而求出G坐标,即可求出OG和OH,用三角函数即可;
(3)先求出点E坐标,从而确定出直线BE解析式,设出点N坐标,用角平分线的性质即可求出m即可.再判断出EN=NA,即可得出结论.
解答 解:(1)∵(a+b)2+(a-4)2=0.
∴a=4,b=-4,
∴A(4,0),B(0,-4),
∵C的坐标为(-1,0),
∴直线BC解析式为y=-4x-4,
∵AH⊥BC,
设直线AH解析式为y=$\frac{1}{4}$x+b,
∵A(4,0)在直线AH上,
∴1+b=0,
∴b=-1,
∴直线AH解析式为y=$\frac{1}{4}$x-1,
∴P(0,-1);
(2)如图2,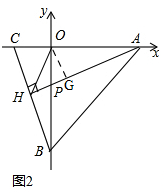
由(1)知,直线BC解析式为y=-4x-4①,
直线AH解析式为y=$\frac{1}{4}$x-1②,
联立①②得H(-$\frac{12}{17}$,-$\frac{20}{17}$)
∴OH2=(-$\frac{12}{17}$)2+(-$\frac{20}{17}$)2=$\frac{544}{289}$,
过点O作OG⊥AH,
∴OG∥BC,
∴直线OG解析式为y=-4x③,
由②③得,G($\frac{4}{17}$,-$\frac{16}{17}$),
∴OG2=($\frac{4}{17}$)2+(-$\frac{16}{17}$)2=$\frac{272}{289}$,
∴$\frac{O{G}^{2}}{O{H}^{2}}=\frac{1}{2}$,
∴$\frac{OG}{OH}=\frac{\sqrt{2}}{2}$,
∴sin∠AHO=$\frac{OG}{OH}=\frac{\sqrt{2}}{2}$,
∴∠AHO=45°,
(3)如图,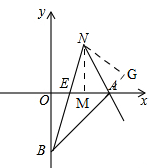
∵S△OEB:S△EAB=1:$\sqrt{2}$,
∴$\frac{OE}{AE}=\frac{1}{\sqrt{2}}$由(1)知,OA=4,
∴OE=4($\sqrt{2}$-1),
∴E(4($\sqrt{2}$-1),0),
∴直线BE解析式为y=($\sqrt{2}$+1)x-4,
设点N(m,($\sqrt{2}$+1)m-4),(m>0)
∴MN=($\sqrt{2}$+1)m-4
∵A(4,0),B(0,-4),
∴直线AB解析式为y=x-4,
∴NG=$\frac{|m-(\sqrt{2}+)m+4-4|}{\sqrt{2}}$=|m|=m,
∵点N在角平分线上,
∴MN=NG.
∴($\sqrt{2}$+1)m-4=m,
∴m=2$\sqrt{2}$,
∴N(2$\sqrt{2}$,2$\sqrt{2}$),
∵A(4,0),E(4($\sqrt{2}$-1),0),
∴AN2=(2$\sqrt{2}$-4)2+(2$\sqrt{2}$)2=32-16$\sqrt{2}$,EN2=[4($\sqrt{2}$-1)-2$\sqrt{2}$]2+(-2$\sqrt{2}$)2=32-16$\sqrt{2}$,
∴AN=EN,
∴∠NEA=∠NAE
∵∠OAB=45°,
∴∠OAG=135°,
∵AN是∠OAG的角平分线,
∴∠EAN=67.5°,
∴∠ANE=180°-∠NEA-∠NAE=45°.
点评 此题三角形综合题,主要考查了非负性,待定系数法,直线的交点坐标,三角函数,角平分线的性质,解本题的关键是用三角函数求出∠AHO,难点是求出点N的坐标


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
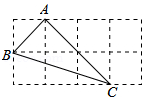 如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m}{n}=\frac{3}{2}$ | B. | $\frac{m}{3}=\frac{n}{2}$ | C. | $\frac{m}{2}=\frac{n}{3}$ | D. | $\frac{2}{n}=\frac{3}{m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-2)2=4 | B. | -[-(5)]=5 | C. | $\frac{2^2}{3}=\frac{4}{9}$ | D. | ${({-3})^2}×({-\frac{1}{3}})=3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数6.91精确到十分位 | |
| B. | 将数80 360用科学计数法表示为80.36×103 | |
| C. | 用四舍五入法得到的近似数17.8350精确到0.001 | |
| D. | 用科学计数法表示的数6.06×104,其原数为60 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com