
【题目】已知点A(-2,2),B(8,12)在抛物线y=ax2+bx上.
(1)求抛物线的解析式;
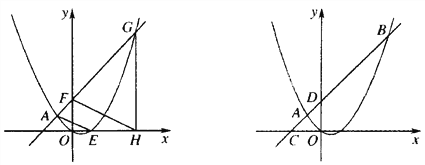
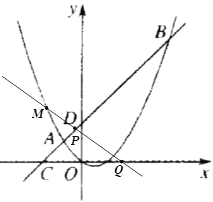
(2)如图1,点F的坐标为(0,m)(m>4),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH、AE,求![]() 之值(用含m的代数式表示);
之值(用含m的代数式表示);
(3)如图2,直线AB分别交x轴、y轴于C、D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒![]() 个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】分析:(1)、根据点A、B的坐标利用待定系数法,即可求出抛物线的解析式;(2)、根据点A、F的坐标利用待定系数法,可求出直线AF的解析式,联立直线AF和抛物线的解析式成方程组,通过解方程组可求出点G的坐标,过A作AN⊥x轴于点N得出点N的坐标,根据方程求出x的值得出答案;(3)、根据点A、B的坐标利用待定系数法,可求出直线AB的解析式,进而可找出点P、Q的坐标,分点M在线段PQ上以及点M在线段QP的延长线上两种情况考虑,借助相似三角形的性质可得出点M的坐标,再利用二次函数图象上点的坐标特征可得出关于t的一元二次方程,解之即可得出结论.
详解:解:(1)、点A(-2,2),B(8,12)在抛物线y=ax2+bx上,∴![]() ∴
∴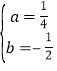 ,∴
,∴![]() ;
;
(2)、设直线AF的解析式为y=kx+m, ∵A(-2,2)在AF上,∴2=-2k+m,k=![]() (m-2),
(m-2),
∴直线y=kx+m可化为![]() , 则
, 则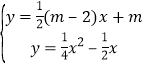
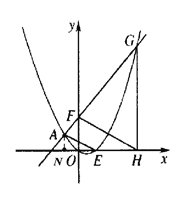
∴x2-2(m-1)x-4m=0, ∴(x+2)(x-2m)=0,∴x=-2或x=2m, ∴G的横坐标为2m,
∴OH=2m,∵OF=m,∴FH=![]() ,过A作AN⊥x轴于点N,则N(-2,0),
,过A作AN⊥x轴于点N,则N(-2,0),
令![]() ,∴x=0或x=2, ∴OE=2,NE=4 ∴AE=
,∴x=0或x=2, ∴OE=2,NE=4 ∴AE=![]() ,∴
,∴![]() ;
;
(3)、由题意A(-2,2),B(8,12),直线AB的解析式为:y=x+4,∠BCO=45°,
直线AB与x轴交点为C(-4,0),设P(t-4,t),则Q(t,0),设M(![]() ,
,![]() )
)
由QM=3PM可得,则|t-![]() |=3|
|=3|![]() -t+4|,
-t+4|,
(ⅰ)当t-![]() =3(
=3(![]() -t+4)即
-t+4)即![]() =t-3,直线PQ的解析式为tx+4y-t2=0,
=t-3,直线PQ的解析式为tx+4y-t2=0,
∴![]() =
=![]() ,∴M(t-3,
,∴M(t-3,![]() ),代入
),代入![]() 即
即![]() ,
,
∴t2-11t+15=0,∴![]() ,即:
,即:![]() ,
,![]() ;
;
(ⅱ)当![]() -t=3(
-t=3(![]() -t+4)即
-t+4)即![]() =t-6,∴
=t-6,∴![]() ,∴
,∴![]() ,
,
代入![]() 即
即![]() ,∴t2-20t+48=0,
,∴t2-20t+48=0,
∴![]() , 即:
, 即:![]() ,
,![]() ;
;
综上所述,所求t为:![]() ,
,![]() ,
,![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题.在进行二次根式去处时,我们有时会碰上如![]() ,
, ![]() ,
, ![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简:
![]() =
=![]() (一)
(一)
![]() =
=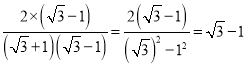 (二)
(二)
以上这种化简的步骤叫做分母有理化.
![]() 还可以用以下方法化简:
还可以用以下方法化简:
![]() =
= (三)
(三)
请用不同的方法化简![]() .
.
(1)参照(二)式得![]() =______________________________________________;
=______________________________________________;
(2)参照(三)式得![]() =_________________________________________。
=_________________________________________。
(3)化简:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=![]() 于点C、D.
于点C、D.
(1)求k、b的值;
(2)写出不等式kx+b>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
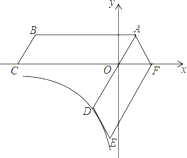
【题目】如图,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,且AO:OD=1:2,点F恰好落在x轴的正半轴上,若点C(﹣6,0),点D在反比例函数y=![]() 的图象上.
的图象上.
(1)证明:△AOF是等边三角形,并求k的值;
(2)在x轴上有一点G,且△ACG是等腰三角形,求点G的坐标;
(3)求旋转过程中四边形ABCO扫过的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内有任意一点![]() 和
和![]() ,按要求解答下列问题:
,按要求解答下列问题:
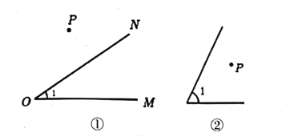
(1)当点![]() 和
和![]() 外部时,如图①,过点
外部时,如图①,过点![]() 作
作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,量一量
,量一量![]() 和
和![]() 的度数,用数学式子表达它们之间的数量关系 ;
的度数,用数学式子表达它们之间的数量关系 ;
(2)当点![]() 在
在![]() 内部时,如图②,以点
内部时,如图②,以点![]() 为顶点作
为顶点作![]() ,使
,使![]() 的两边分别和
的两边分别和![]() 的两边垂直,垂足分别为
的两边垂直,垂足分别为![]() 、
、![]() ,用数学式子写出
,用数学式子写出![]() 和
和![]() 的数量关系;
的数量关系;
(3)由上述情形,用文字语言叙述结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 .
(4)在图②中,若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
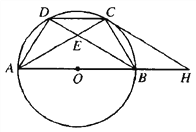
【题目】如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;
(2)若AE=2EC,求![]() 之值;
之值;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=![]() ,求EC之长.
,求EC之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京市积极开展城市环境建设,其中污水治理是重点工作之一,以下是北京市2012﹣2017年污水处理率统计表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
污水处理率(%) | 83.0 | 84.6 | 86.1 | 87.9 | 90.0 | 92.0 |
(1)用折线图将2012﹣2017年北京市污水处理率表示出来,并在图中标明相应的数据;
(2)根据统计图表中提供的信息,预估2018年北京市污水处理率约为_____%,说明你的预估理由:_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com