
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A��B��C������ֱ�Ϊ��0��5������0��2������4��2����ֱ��l�Ľ���ʽΪy=kx+5-4k��k��0����
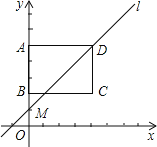
��1����ֱ��l������Bʱ����һ�κ����Ľ���ʽ��
��2��ͨ������˵��������kΪ��ֵ��ֱ��l�ܾ�����D��
��3��ֱ��l��y�ύ�ڵ�M����N���߶�DM�ϵ�һ�㣬����NBDΪ���������Σ���̽����������y=kx+5-4kΪ����������ʱ����N�ĸ�����______����
���𰸡���1��y=![]() x+2����2�������������3��2.
x+2����2�������������3��2.
��������
��1������B����������ʽ����⣻
��2��������ɵõ�D��4��5������y=kx+5-4k=k��x-4��+5��֪����x-4=0ʱ������kΪ��ֵ��ֱ��l�ܾ����㣨4��5�������ɵý��ۣ�
��3�����������k=![]() ���������O���M�غϣ����������ε����ʿ����N�ĸ�����
���������O���M�غϣ����������ε����ʿ����N�ĸ�����
�⣺��1����ֱ��l������B��0��2����
��2=5-4k
��k=![]()
��һ�κ�������ʽΪ��y=![]() x+2
x+2
��2����A��B��C������ֱ�Ϊ��0��5������0��2������4��2����
���D��4��5��
��y=kx+5-4k=k��x-4��+5
�൱x=4ʱ��y=5��
���kΪ��ֵ��ֱ��l�ܾ����㣨4��5��
������kΪ��ֵ��ֱ��l�ܾ�����D��
��3���ߺ���y=kx+5-4kΪ����������
��5-4k=0
��k=![]()
�ຯ������ʽΪ��y=![]() x
x
���M���O�غϣ���ͼ����BM=2
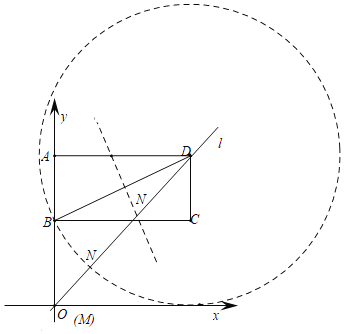
�ߡ�NBDΪ���������Σ�
����BD�Ĵ�ֱƽ���߽�DO�ڵ�N�����Ե�DΪԲ�ģ�BDΪ�뾶��Բ�����߶�DO�ڵ�N
���N�ĸ���Ϊ2��
�ʴ�Ϊ��2


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
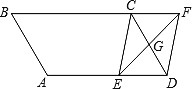
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB=4cm��BC=6cm����B=60����G��CD���е㣬E�DZ�AD�ϵĶ���(E����A��D�غ�)���ҵ�E��A��D�˶����ٶ�Ϊ1cm/s��EG���ӳ�����BC���ӳ��߽��ڵ�F������CE��DF�����E���˶�ʱ��Ϊ![]()
(1)��֤:����![]() Ϊ��ֵ,�ı���CEDF����ƽ���ı��Σ�
Ϊ��ֵ,�ı���CEDF����ƽ���ı��Σ�
(2)�ٵ�![]() sʱ,CE��AD��
sʱ,CE��AD��
�ڵ�![]() ʱ,ƽ���ı���CEDF�������ڱ����.
ʱ,ƽ���ı���CEDF�������ڱ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1���ⲻ��ʽ2x+9��3��x+2��
��2���ⲻ��ʽ�飺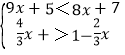 ����д���������⣮
����д���������⣮
��3����֪��Ԫһ�η�����![]() �Ľ�x��y����������
�Ľ�x��y����������
����a��ȡֵ��Χ��
������|4a+5|��|a��4|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������У���ABCΪ��������Σ����㶼�Ǹ�㣩������ABC�Ƶ�A����ʱ�뷽����ת90���õ���AB1C1��
��1����������������������AB1C1��
��2��������С�����εı߳�Ϊ1������ת�����ж���B��������·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������A�ؿ���B�أ�һ��С������B�ؿ���A�أ�ͬʱ��������������ʻ�����Ե����յ��ֹͣ���������С����֮��ľ���Ϊs��ǧ�ף���������ʻ��ʱ��Ϊt��Сʱ����S��t֮��ĺ�����ϵ��ͼ��ʾ������˵������ȷ���У� ��
��A��B�������60ǧ�ף�
������1Сʱ��������С����������
��С�������ٶ��ǻ����ٶȵ�2����
������1.5Сʱ��С�����Ȼ�������ʻ��60ǧ�ף�
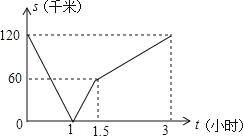
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̶�м�2017��ɹ�����ȫ����������֮����������ȫ���������У�ijС��������Ӧ��������С���ڰ�װ�����������ܰ��ʾ�ƺ������䣬������2����ܰ��ʾ�ƺ�3�������乲��550Ԫ����������ĵ�������ܰ��ʾ�Ƶ��۵�3����
��1������ܰ��ʾ�ƺ�������ĵ��۸��Ƕ���Ԫ��
��2����С��������Ҫ����48�������䣬���������ܰ��ʾ�ƺ������乲100�����ҷ��ò�����10000Ԫ�������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
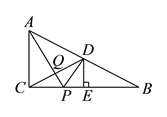
����Ŀ����ͼ����![]() �У�
�� ![]() ����
����![]() ��
��![]() �ߵ��е㣬��
�ߵ��е㣬��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �DZ�
�DZ�![]() �ϵ�һ�����㣬
�ϵ�һ�����㣬 ![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��ֵ��Сʱ��
��ֵ��Сʱ�� ![]() ��
��![]() ֮���������ϵ��__________��
֮���������ϵ��__________��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�F��AD���е㣬�ӳ�BC����E��ʹCE=![]() BC������DE��CF��
BC������DE��CF��
��1����֤���ı���CEDF��ƽ���ı��Σ�
��2����AB=4��AD=6����B=60������DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����֪A����1��0����C��0��3��
��1����������ߵı���ʽ��
��2����BC�Ľ���ʽ��
��3����M�ǶԳ����Ҳ��B������������һ�����㣬����M�˶���ʲôλ��ʱ����BCM������������BCM��������ֵ����ʱ��M�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com