
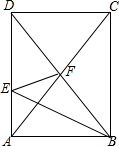
 如图,矩形ABCD的面积为36,BE平分∠ABD,交AD于E,沿BE将△ABE折叠,点A的对应点刚好落在矩形两条对角线的交点F处,则△ABE的面积为6.
如图,矩形ABCD的面积为36,BE平分∠ABD,交AD于E,沿BE将△ABE折叠,点A的对应点刚好落在矩形两条对角线的交点F处,则△ABE的面积为6. 分析 首先证明△AEB≌△FEB≌△DEF,从而可知△ABE的面积=$\frac{1}{3}{S}_{△DAB}$,从而可求得△ABE的面积.
解答 解:由翻折的性质可知:△AEB≌△FEB.
∴∠EFB=∠EAB=90°.
∵ABC为矩形,
∴DF=FB.
∴EF垂直平分DB.
∴ED=EB.
在△DEF和△BEF中,
$\left\{\begin{array}{l}{DF=BF}\\{EF=EF}\\{ED=EB}\end{array}\right.$,
∴△DEF≌△BEF.
∴△AEB≌△FEB≌△DEF.
∴△ABE的面积=$\frac{1}{3}{S}_{△DAB}=\frac{1}{3}×\frac{1}{2}×36$=6.
故答案为:6.
点评 本题主要考查的是翻折的性质、矩形的性质、线段垂直平分线的性质和判定、全等三角形的判定和性质,证得△AEB≌△FEB≌△DEF是解题的关键.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:填空题
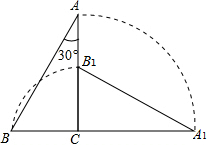 如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$.
如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
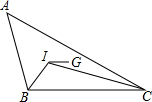 如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
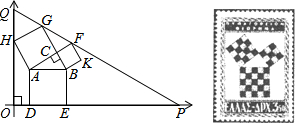
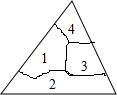 小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )| A. | 第1块 | B. | 第2块 | C. | 第3块 | D. | 第4块 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米.
如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
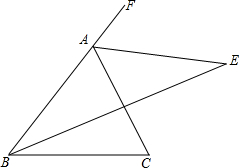 如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.
如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com