
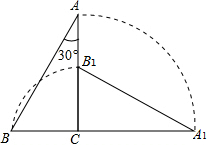
 如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$.
如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$. 分析 根据直角三角形的性质求出BC、AC的长度,设点B扫过的路线与AB的交点为D,连接CD,可以证明△BCD是等边三角形,然后求出点D是AB的中点,所以△ACD的面积等于△ABC的面积的一半,然后根据△ABC扫过的面积=S扇形ACA1+S扇形BCD+S△ACD,然后根据扇形的面积公式与三角形的面积公式列式计算即可得解.
解答 解:在△ABC中,∠ACB=90°,∠BAC=30°,AB=4,
∴BC=$\frac{1}{2}$AB=2,∠B=90°-∠BAC=60°,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=2$\sqrt{3}$,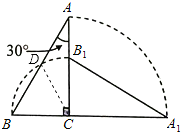
∴S△ABC=$\frac{1}{2}$×BC×AC=2$\sqrt{3}$,
设点B扫过的路线与AB的交点为D,连接CD,
∵BC=DC,
∴△BCD是等边三角形,
∴BD=CD=2,
∴点D是AB的中点,
∴S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
∴△ABC扫过的面积=S扇形ACA1+S扇形BCD+S△ACD,
=$\frac{90}{360}$×π×(2$\sqrt{3}$)2+$\frac{60}{360}$×π×22+$\sqrt{3}$,
=$\frac{11}{3}$π+$\sqrt{3}$.
故答案为:$\frac{11}{3}$π+$\sqrt{3}$.
点评 此题考查了扇形面积的计算、旋转的性质、直角三角形的性质以及等边三角形的性质,注意掌握旋转前后图形的对应关系,利用数形结合思想把扫过的面积分成两个扇形的面积与一个三角形面积是解题的关键,也是本题的难点.


科目:初中数学 来源: 题型:填空题
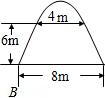 如图,某学校的校门是一抛物线形状的建筑物,地面宽度为8m,两侧距地面6m高处各有一个挂校名横匾用的铁环,两铁环的水平距离为4m,则校门的高度为8m.
如图,某学校的校门是一抛物线形状的建筑物,地面宽度为8m,两侧距地面6m高处各有一个挂校名横匾用的铁环,两铁环的水平距离为4m,则校门的高度为8m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
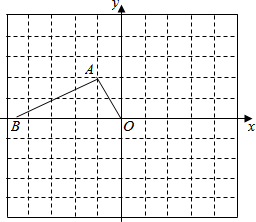 如图,在Rt△AOB中,∠A=90°,∠AOB=60°,在边长为1的小正方形组成的网格中,△AOB的顶点O、A均在格点上,点B在x轴上,点A的坐标为(-1,2).
如图,在Rt△AOB中,∠A=90°,∠AOB=60°,在边长为1的小正方形组成的网格中,△AOB的顶点O、A均在格点上,点B在x轴上,点A的坐标为(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
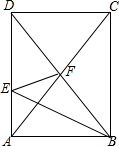 如图,矩形ABCD的面积为36,BE平分∠ABD,交AD于E,沿BE将△ABE折叠,点A的对应点刚好落在矩形两条对角线的交点F处,则△ABE的面积为6.
如图,矩形ABCD的面积为36,BE平分∠ABD,交AD于E,沿BE将△ABE折叠,点A的对应点刚好落在矩形两条对角线的交点F处,则△ABE的面积为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com