
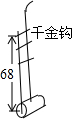
 中国民间乐器二胡的“千斤钩”钩在弦长的黄金分割点处音质最好,一把二胡的弦长为68cm,求“千金钩”上、下两部分弦长.
中国民间乐器二胡的“千斤钩”钩在弦长的黄金分割点处音质最好,一把二胡的弦长为68cm,求“千金钩”上、下两部分弦长.  初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:填空题
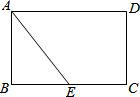 如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是$\frac{18}{5}$ cm.
如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是$\frac{18}{5}$ cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
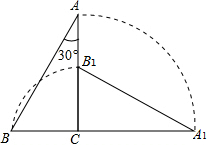 如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$.
如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
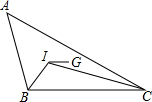 如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米.
如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com