
科目:初中数学 来源: 题型:解答题
 (1)(-$\frac{1}{2}$)-2+|$\sqrt{3}$-3|-$\root{3}{27}$+tan60°
(1)(-$\frac{1}{2}$)-2+|$\sqrt{3}$-3|-$\root{3}{27}$+tan60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
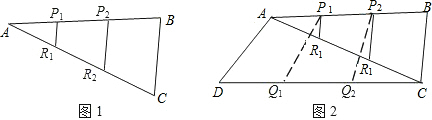
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
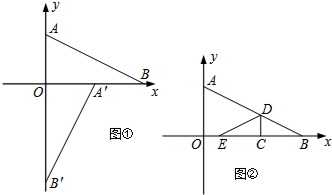
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某住宅小区为缓解停车难问题,新建了地下停车场,建筑设计师提供了地下停车场的设计示意图.按规定,停车场坡道口要张贴限高标志,以便告知车辆能否安全驶入.请根据如图,求出汽车通过坡道口的限高CF的长($\sqrt{3}$≈1.73,结果精确到0.1m).
某住宅小区为缓解停车难问题,新建了地下停车场,建筑设计师提供了地下停车场的设计示意图.按规定,停车场坡道口要张贴限高标志,以便告知车辆能否安全驶入.请根据如图,求出汽车通过坡道口的限高CF的长($\sqrt{3}$≈1.73,结果精确到0.1m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com