
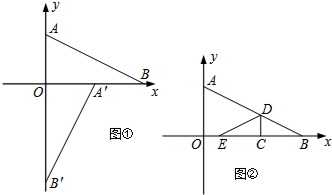
分析 (1)根据旋转的性质可以得到OA=OA′,OB=OB′,则A,B的坐标就可以得到.
(2)(Ⅰ)OB=4,C点的位置应分两种情况进行讨论:当C在OB的中点或在中点与B之间时,重合部分是△CDE;当C在OB的中点与O之间时,重合部分是梯形,就可以得到函数解析式.
(Ⅱ)分△ADE以点A为直角顶点和△ADE以点E为直角顶点的两种情况进行讨论.根据相似三角形的对应边的比相等,求出OE的长,就可以得到C点的坐标.
解答 解:(1)∵点A′,B′的坐标分别为(2,0)和(0,-4),将△A′B′O绕点O按逆时针方向旋转90°后得△ABO,点A'的对应点是点A,点B′的对应点是点B,
∴A(0,2),B(4,0);
(2)(Ⅰ)①点E在原点和x轴正半轴上时,重叠部分是△CDE.
则S△CDE=$\frac{1}{2}$BC×CD=$\frac{1}{2}$(4-x)(-$\frac{1}{2}$x+2)=$\frac{1}{4}$x2-2x+4,
当E与O重合时,CE=$\frac{1}{2}$BO=2,
∴2≤x<4;
②当E在x轴的负半轴上时,设DE与y轴交于点F,则重叠部分为梯形
∵△OFE∽△OAB,
∴$\frac{OF}{OE}$=$\frac{OA}{OB}$=$\frac{1}{2}$,
∴OF=$\frac{1}{2}$OE,
又∵OE=4-2x,
∴OF=$\frac{1}{2}$(4-2x)=2-x
∴S四边形CDFO=$\frac{x}{2}$×[2-x+(-$\frac{1}{2}$x+2)]=-$\frac{3}{4}$x2+2x,
当点C与点O重合时,点C的坐标为(0,0),
∴0<x<2.
综合①②得S=$\left\{\begin{array}{l}{\frac{1}{4}{x}^{2}-2x+4(2≤x<4)}\\{-\frac{3}{4}{x}^{2}+2x(0<x<2)}\end{array}\right.$;
(Ⅱ)存在,点C的坐标为($\frac{3}{2}$,0)和($\frac{5}{2}$,0).
解:①如图,当△ADE以点A为直角顶点时,作AE⊥AB交x轴负半轴于点E,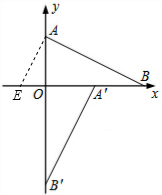
∵△AOE∽△BOA
∴$\frac{EO}{AO}$=$\frac{AO}{BO}$=$\frac{1}{2}$,
∵AO=2,
∴EO=1,
∴点E坐标为(-1,0),
∴点C的坐标为($\frac{3}{2}$,0);
②当△ADE以点E为直角顶点时,
同样有△AOE∽△BOA,
$\frac{EO}{AO}$=$\frac{AO}{BO}$=$\frac{1}{2}$,
∴EO=1,
∴E(1,0).
∴点C的坐标($\frac{5}{2}$,0).
综合①②知满足条件的点C坐标有($\frac{3}{2}$,0)和($\frac{5}{2}$,0).
点评 本题主要考查了几何变换综合题,涉及的知识点有:几何图形的面积计算,相似三角形的性质:对应边的比相等,以及分类思想的应用,综合性较强,有一定的难度.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
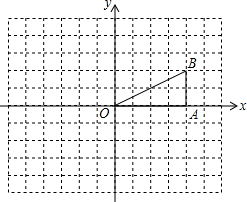 如图,在△OAB中,∠OAB=90°,且点B的坐标为(4,2).
如图,在△OAB中,∠OAB=90°,且点B的坐标为(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 357×104 | B. | 3.57×107 | C. | 35.7×105 | D. | 3.57×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-6|=6 | B. | $(\frac{1}{2})^{-1}=-2$ | C. | $\sqrt{16}=±4$ | D. | a2•a3=a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com