
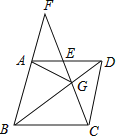
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据菱形的性质得到AB∥CD,AD=CD,∠ADB=∠CDB,推出△ADG≌△CDG,根据全等三角形的性质即可得到结论;
(2)由全等三角形的性质得到∠EAG=∠DCG,等量代换得到∠EAG=∠F,求得△AEG∽△FGA,即可得到结论.
解:(1)∵四边形ABCD是菱形,
∴AB∥CD,AD=CD,∠ADB=∠CDB,
在△ADG与△CDG中,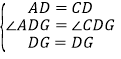 ,
,
∴△ADG≌△CDG(SAS),
∴AG=CG;
(2)∵△ADG≌△CDG,AB∥CD
∴∠F=∠FCD,∠EAG=∠GCD,
∴∠EAG=∠F
∵∠AGE=∠AGE,
∴△AEG∽△FAG,
∴![]() ,
,
∴AG2=GEGF.


科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至ED,连接AE、DE,△ADE的面积为3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)在这个问题中,总体指的是?个体指的是?样本是?样本容量是?
(2)试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
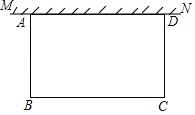
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为______.
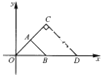
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知经过原点的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() ,现将抛物线向右平移
,现将抛物线向右平移![]() 个单位长度,所得抛物线与
个单位长度,所得抛物线与![]() 轴交于
轴交于![]() ,与原抛物线交于点
,与原抛物线交于点![]() ,设
,设![]() 的面积为
的面积为![]() ,则用
,则用![]() 表示
表示![]() =__________
=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com