
分析 (1)由月销售利润=每千克的利润×可卖出千克数,把相关数值代入即可;
(2)根据“月销售利润为8000元”列出一元二次方程,解之可得答案;
(3)将函数解析式配方成顶点式可得二次函数的最值.
解答 解:(1)可卖出千克数为500-10(x-50)=1000-10x,
y与x的函数表达式为y=(x-40)(1000-10x)=-10x2+1400x-40000;
(2)根据题意得-10x2+1400x-40000=8000,
解得:x=60或x=80,
答:当售价定为60元或80元时,该商店月销售利润为8000元;
(3)∵y=(x-40)[500-10(x-50)]=-10x2+1400x-40000=-10(x-70)2+9000,
∴当x=70时,利润最大为9000元.
答:当售价为70元,利润最大,最大利润是9000元.
点评 本题主要考查了二次函数的应用及解一元二次方程的能力,能正确表示出月销售量是解题的关键.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.


科目:初中数学 来源: 题型:填空题
 定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.若AM=2,MN=3,则BN的长为$\sqrt{3}$或$\sqrt{15}$.
定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.若AM=2,MN=3,则BN的长为$\sqrt{3}$或$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
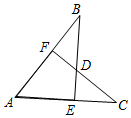 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的有①②③.
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的有①②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com