练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知，如图，△ABC 中，D 是 BC 的中点，AB＝5，AC＝3，AD＝2．

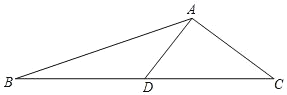
    （1）按要求画图：延长 AD 至点 E，使 DE＝AD，连接 BE；

    （2）求 BC 的长度．

    【答案】（1）见解析；（2）

    【解析】

    （1）根据几何语言画出对应的图形即可；

    （2）先证明△BDE≌△CDA，得到BE＝AC＝3，再利用勾股定理的逆定理证明△ABE为直角三角形，∠AEB＝90°，然后根据勾股定理计算出BD，从而得到BC的长．

    解：（1）如图所示；

    （2）∵D 是 BC 的中点，

    ∴BD＝CD，

    在△BDE 和△CDA 中，，

    ∴△BDE≌△CDA，

    ∴BE＝AC＝3，

    ∵AE＝2AD＝4，AB＝5，

    ∴AE2＋BE2＝AB2，

    ∴△ABE 为直角三角形，∠AEB＝90°，

    在Rt△BDE中，BD＝，

    ∴BC＝2BD＝．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

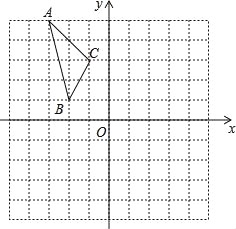
    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．

    （1）若△ABC经过平移后得到，已知点的坐标为（4，0），写出顶点，的坐标；

    （2）若△ABC和关于原点O成中心对称图形，写出的各顶点的坐标；

    （3）将△ABC绕着点O按顺时针方向旋转90°得到，写出的各顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有两个关于x的一元二次方程：M： N：，其中，以下列四个结论中，错误的是（ ）

    A. 如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根；

    B. 如果方程M有两根符号异号，那么方程N的两根符号也异号；

    C. 如果5是方程M的一个根，那么是方程N的一个根；

    D. 如果方程M和方程N有一个相同的根，那么这个根必定是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知某种产品的进价为每件40元，现在的售价为每件60元，每星期可卖出300件．市场调查发现，该产品每降价1元，每星期可多卖出20件，由于供货方的原因销量不得超过380件，设这种产品每件降价x元（x为整数），每星期的销售利润为w元．

    （1）求w与x之间的函数关系式，并写出自变量x的取值范围；

    （2）该产品销售价定为每件多少元时，每星期的销售利润最大？最大利润是多少元？

    （3）该产品销售价在什么范围时，每星期的销售利润不低于6000元，请直接写出结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点A（x1，0）、B（x2，0），我们把|x1﹣x2|记为d（A、B），抛物线的顶点到x轴的距离记为d（x），如果d（A，B）=d（x），那么把这样的抛物线叫做“正抛物线”．

    （1）抛物线y=2x2﹣2是不是“正抛物线”；（回答“是”或“不是”）．

    （2）若抛物线y=﹣x2+bx（b＞0）是“正抛物线”，求抛物线的解析式；

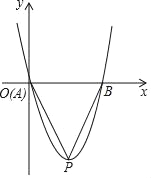
    （3）如图，若“正抛物线”y=x2+mx（m＜0）与x轴相交于A、B两点，点P是抛物线的顶点，则抛物线上是否存在点C，使得△PAC是以PA为直角边的直角三角形？如果存在，请求出C的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以O为原点的直角坐标系中，A点的坐标为（0，1），直线x=1交x轴于点B．点为线段AB上一动点，作直线PC⊥PO，交直线x=1于点C．过P点作直线MN平行于x轴，交y轴于点M，交直线x=1于点N．记AP=x，△PBC的面积为S．

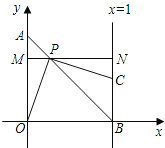
    （1）当点C在第一象限时，求证：△OPM≌△PCN；

    （2）当点P在线段AB上移动时，点C也随之在直线x=1上移动，求出S与x之间的函数关系式，并写出自变量的取值范围；

    （3）当点P在线段AB上移动时，△PBC是否可能成为等腰三角形？如果可能，直接写出所有能使△PBC成为等腰三角形的x的值；如果不可能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在社会主义新农村建设中，某乡镇决定对一段公路进行改造，已知这项工程由甲工程队单独做需要40天完成；如果由乙工程先单独做10天，那么剩下的工程还需要两队合做20天才能完成．

    （1）求乙工程队单独完成这项工程所需的天数；

    （2）求两队合作完成这项工程所需的天数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

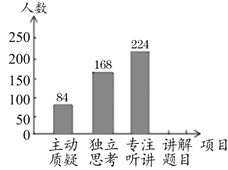
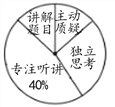
    【题目】某地区教育部门为了解初中数学课堂中学生参与情况，并按“主动质疑、独立思考、专注听讲、讲解题目”四个项目进行评价．检测小组随机抽查部分学校若干名学生，并将抽查学生的课堂参与情况绘制成如图所示的扇形统计图和条形统计图（均不完整）．请根据统计图中的信息解答下列问题：

    （1）本次抽查的样本容量是 ；

    （2）在扇形统计图中，“主动质疑”对应的圆心角为 度；

    （3）将条形统计图补充完整；

    （4）如果该地区初中学生共有60000名，那么在课堂中能“独立思考”的学生约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数的图象经过点P（2，﹣3）．

    （1）求该函数的解析式；

    （2）若将点P沿x轴负方向平移3个单位，再沿y轴方向平移n（n＞0）个单位得到点P′，使点P′恰好在该函数的图象上，求n的值和点P沿y轴平移的方向．

    查看答案和解析>>

    同步练习册答案