
【题目】如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点A(x1,0)、B(x2,0),我们把|x1﹣x2|记为d(A、B),抛物线的顶点到x轴的距离记为d(x),如果d(A,B)=d(x),那么把这样的抛物线叫做“正抛物线”.
(1)抛物线y=2x2﹣2是不是“正抛物线”;(回答“是”或“不是”).
(2)若抛物线y=﹣x2+bx(b>0)是“正抛物线”,求抛物线的解析式;
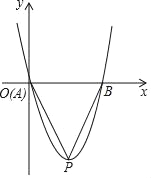
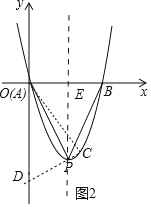
(3)如图,若“正抛物线”y=x2+mx(m<0)与x轴相交于A、B两点,点P是抛物线的顶点,则抛物线上是否存在点C,使得△PAC是以PA为直角边的直角三角形?如果存在,请求出C的坐标;若不存在,请说明理由.
【答案】(1)抛物线y=2x2﹣2是“正抛物线”;(2)抛物线的解析式为y=﹣x2+4x;(3)满足条件的点C坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)根据“正抛物线”的定义判断即可;
(2)根据“正抛物线”的定义构建方程即可解决问题;
(3)首先求出m,分两种情形分别求解即可解决问题;
(1)对于抛物线y=2x2﹣2,
当y=0时,2x2﹣2=0,解得x=1或﹣1,
∴A(﹣1,0),B(1,0),
∴d(A,B)=2,
![]()
∴d(x)=d(A,B),
∴抛物线y=2x2﹣2是“正抛物线”.
故答案为:是.
(2)当y=0时,﹣x2+bx=0,解得x=0或b,
∵b>0,
∴d(A,B)=b,
由题意![]()
解得b=0(舍弃)或b=4,
∴抛物线的解析式为![]()
(3)当y=0时,x2+mx=0,解得x=0或﹣m,
∵m<0,
∴d(A,B)![]()
∵![]()
∴d(x)![]()
由题意![]()
解得![]() 或0(舍弃),
或0(舍弃),
∴![]()
假设存在点C,使得△PAC是以PA为直角边的直角三角形,分两种情形:
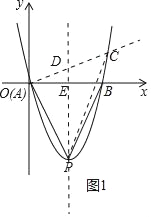
①如图1中,作AC⊥AP交抛物线于点C,厉害PC,作PE⊥x轴交AC于D.
![]()
∴AE=2,PE=4,
由△ADE∽△PAE,可得![]()
∴![]()
∴DE=1,
∴D(2,1),
∴直线AD的解析式为![]()
由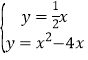 解得
解得![]() 或
或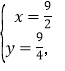
∴![]()
②如图2中,作PC⊥AP交抛物线于C,交y轴于D,连接AC,作PE⊥x轴于E.
由△ADP∽△PAE,可得![]() 即
即![]()
∴![]()
∴AD=5,
∴D(0,5),
∴直线AD的解析式为![]()
由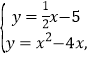 解得
解得![]() 或
或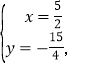
综上所述,满足条件的点C坐标为(92,94)或(52,154).
综上所述,满足条件的点C坐标为![]() 或
或![]()


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC 中,D 是 BC 的中点,AB=5,AC=3,AD=2.
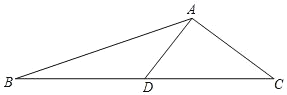
(1)按要求画图:延长 AD 至点 E,使 DE=AD,连接 BE;
(2)求 BC 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则,等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化作整式与真分式的和的形式.
如:![]() ;
;![]()
(1)下列分式中,属于真分式的是__________(填序号);
①![]() ②
②![]() ③
③![]() ④
④![]()
(2)将假分式![]() 化为整式与真分式的和的形式:
化为整式与真分式的和的形式:![]() __________;若假分式
__________;若假分式![]() 的值为正整数,则整数
的值为正整数,则整数![]() 的值为__________;
的值为__________;
(3)请你写出假分式![]() 化成整式与真分式的和的形式的完整过程.
化成整式与真分式的和的形式的完整过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
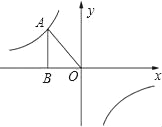
【题目】如图,已知反比例函数y=![]() (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com