
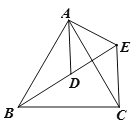
【题目】如图,△ ABC 和△ADE都是等边三角形,点 B 在 ED 的延长线上.
(1)求证:△ABD≌△ACE.
(2)求证:AE+CE=BE.
(3)求∠BEC 的度数.
【答案】(1)见解析;(2)见解析;(3)∠BEC=60°.
【解析】
(1)由等边三角形的性质可得AB=AC,AD=AE,∠BAC=∠DAE=60°,继而可得∠BAD=∠CAE,利用SAS即可证得△ABD≌△ACE;
(2)由全等三角形的性质可得BD=CE,再由DE=AE即可证得结论;
(3)由等边三角形的性质可得∠ADE=∠AED=60°,从而可得∠ADB=120°,由△ABD≌△ACE ,可得∠AEC=∠ADB=120°,由此即可求得答案.
(1)∵△ ABC 和△ADE 都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE;
(2)∵△ABD≌△ACE,
∴BD=CE,
∵△ADE 是等边三角形,
∴DE=AE,
∵DE+BD=BE,
∴AE+CE=BE;
(3)∵△ADE 是等边三角形,∴∠ADE=∠AED=60°,
∴∠ADB=180°-∠ADE=180°-60°=120°,
∵△ABD≌△ACE ,
∴∠AEC=∠ADB=120°,
∴∠BEC=∠AEC-∠AED=120°-60°=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.

(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究问题:已知![]() ,画一个角
,画一个角![]() ,使
,使![]() ,且
,且![]() 交
交![]() 于点
于点![]() .
.![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?

(1)我们发现![]() 与
与![]() 有两种位置关系:如图1与图2所示.
有两种位置关系:如图1与图2所示.
①图1中![]() 与
与![]() 数量关系为____________;图2中
数量关系为____________;图2中![]() 与
与![]() 数量关系为____________.请选择其中一种情况说明理由.
数量关系为____________.请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述):____________________________.
(2)应用②中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为16海里.求A、C两地之间的距离.(保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E.
(1)求证:D为BC的中点;
(2)过点O作OF⊥AC,于F,若AF=![]() ,BC=2,求⊙O的直径.
,BC=2,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(4分)一元二次方程![]() 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
【答案】A.
【解析】
试题∵△=![]() ,∴方程有两个不相等的实数根.故选A.
,∴方程有两个不相等的实数根.故选A.
考点:根的判别式.
【题型】单选题
【结束】
9
【题目】已知直线y=kx(k>0)与双曲线![]() 交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
A.﹣6 B.﹣9 C.0 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数![]() 和
和![]() 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥
的图象上,PC⊥![]() 轴于点C,交
轴于点C,交![]() 的图象于点A,PC⊥
的图象于点A,PC⊥![]() 轴于点D,交
轴于点D,交![]() 的图象于点B. 当点P在
的图象于点B. 当点P在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①![]()
②![]() 的值不会发生变化
的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com