
【题目】已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.
(1)如图1,若AB=![]() ,点A,E,P恰好在一条直线上时,求EF的长(直接写出结果);
,点A,E,P恰好在一条直线上时,求EF的长(直接写出结果);
(2)如图2,当点P为射线BC上任意一点时,求证:BF=EF;
(3)若AB=![]() ,设BP=2,求QF的长.
,设BP=2,求QF的长.

【答案】(1)1;(2)见解析;(3)3.
【解析】
(1)根据A、E、P在同一直线上判断出点E是AP的中点,先根据直角三角形30°角所对的直角边等于斜边的一半求出AP,然后根据等边三角形的性质求出QE.再根据直角三角形的性质求出QF,然后根据EF=QF﹣QE,代入数据进行计算即可;(2)先求出∠BAP=∠EAQ,然后利用“边角边”证明△ABP≌△AEQ,根据全等三角形对应角相等可得∠AEQ=∠ABP=90°,然后求出∠BEF=∠EBF=30°,再根据等角对等边的性质即可得证;(3)过点F作FD⊥BE于点D,根据等腰三角形三线合一的求出BD,再解直角三角形求出BF的长度,即可得到EF的长,再根据全等三角形对应边相等可得QE=BP,然后代入数据进行计算即可.
解:(1)∵△ABE是等边三角形,A、E、P在同一直线上,
∴AB=AE,∠BAE=60°,
∴∠APB=30°,
∴AP=2AB=2![]() ,
,
∴点E是AP的中点,
∴QE⊥AP,
∴QE=3,
∵∠APQ=60°,∠APB=30°,
∴∠QPF=90°,
∴QF=4,
∴EF=QF﹣QE=1;
(2)证明:∵∠BAP=∠BAE﹣∠EAP=60°﹣∠EAP,
∠EAQ=∠QAP﹣∠EAP=60°﹣∠EAP,
∴∠BAP=∠EAQ.
在△ABP和△AEQ中,
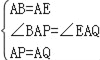 ,
,
∴△ABP≌△AEQ(SAS),
∴∠AEQ=∠ABP=90°,
∴∠BEF=180°﹣∠AEQ﹣∠AEB=180°﹣90°﹣60°=30°,
∵∠EBF=90°﹣60°=30°,
∴∠BEF=∠EBF,
∴EF=BF;
(3)如图,过点F作FD⊥BE于点D,
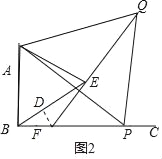
∵△ABE是等边三角形,
∴BE=AB=![]() ,
,
由(2)得∠EBF=30°,
在Rt△BDF中,BD=![]() BE=
BE=![]() ,
,
∴BF=![]() =1,
=1,
∴EF=1,
∵△ABP≌△AEQ,
∴QE=BP=2,
∴QF=QE+EF=2+1=3.


科目:初中数学 来源: 题型:
【题目】如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC. 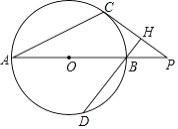
(1)求证:PC是⊙O的切线;
(2)若sin∠P= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y= ![]() x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究 ![]() 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有两条边长的比值为 ![]() 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出 ![]() 的值为;
的值为;
(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°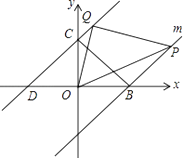
(1)则∠PBO=度;
(2)问:PBCQ的值是否为定值?如果是,请求出该定值;如果不是,请说明理由;
(3)求证:CQ2+PB2=PQ2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名射击运动员连续打靶8次,命中的环数如图所示,则命中环数的众数与中位数分别为( ) 
A.9环与8环
B.8环与9环
C.8环与8.5环
D.8.5环与9环
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,BC=4cm,AC=3cm,把△ABC绕点A顺时针旋转90°后,得到△A1B1C1(如图所示),则线段AB所扫过的面积为( ) 
A.5 ![]()
B.![]() πcm2
πcm2
C.![]() πcm2
πcm2
D.5πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):

(1)当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费________元(用含a、n的整式表示);
(3)当a=2时,甲、乙两用户一个月共用水40m3 ,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3 ,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com