
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣2x﹣3a与x轴交于A、B两点,与y轴交于C点,OC=OB,点P为抛物线上一动点
(1)求抛物线的解析式;
(2)当点P运动到抛物线对称轴右侧时如图2,连PC、BC、BP得△BCP.设△BCP的面积为s,点P的横坐标为x.若s<![]() ,求x的取值范围;
,求x的取值范围;
(3)当点P运动到第四象限时,连AP、BP,BP交y轴于点R,过B作直线l∥AP交y轴于点Q,问:QR、OC之间是否存在确定的数量关系?若存在,请求出并证明;若不存在,请说明理由.

【答案】(1)y=x2﹣2x﹣3;(2)1<x<![]() 且x≠
且x≠![]() ;(3)存在,RQ=4OC,见解析
;(3)存在,RQ=4OC,见解析
【解析】
(1)由已知可求A(﹣1,0),B(3,0),C(0,﹣3),所以﹣3a=﹣3,即a=1;
(2)当点P在x轴下方时,设P(x,x2﹣2x﹣3),过点P作PQ∥y轴,交BC于点Q,求得直线BC的解析式为y=x﹣3,所以Q(x,x﹣3),表示出S![]() ,当S=
,当S=![]() 时,
时,![]() ,当点P在x轴上时,同理可得,
,当点P在x轴上时,同理可得,![]() 时,
时,![]() ;由已知并结合图象可得,1<x<
;由已知并结合图象可得,1<x<![]() 且x≠
且x≠![]() ;
;
(3)设直线AP的解析式为y=kx+k,联立方程组![]() ,可得xp=3+k,设直线BP的解析式为y=mx﹣3m,联立方程组
,可得xp=3+k,设直线BP的解析式为y=mx﹣3m,联立方程组![]() ,可得xp+3=m+2,则有m﹣k=4,设直线BQ的解析式为y=kx﹣3k,分别得到Q(0,﹣3k),R(0.﹣3m),则可得RQ=4OC.
,可得xp+3=m+2,则有m﹣k=4,设直线BQ的解析式为y=kx﹣3k,分别得到Q(0,﹣3k),R(0.﹣3m),则可得RQ=4OC.
(1)由已知可求A(﹣1,0),B(3,0),
∵OC=OB,
∴C(0,﹣3),
∴﹣3a=﹣3,
∴a=1,
∴y=x2﹣2x﹣3;
(2)当点P在x轴下方时,设P(x,x2﹣2x﹣3),过点P作PQ∥y轴,交BC于点Q,
求得直线BC的解析式为y=x﹣3,
∴Q(x,x﹣3),
∴![]() ,即
,即![]() ,
,
当S=![]() 时,
时,![]() ,
,
化简得:![]() ,即:
,即:![]() ,
,
∴![]() ,
,
当点P在x轴上时,同理可得,
![]() 时,
时,![]() ;
;
∵P点在对称轴的右侧,
∴当S<![]() 时,由图象可得,1<x<
时,由图象可得,1<x<![]() 且x≠
且x≠![]() ;
;
(3)设直线AP的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 的坐标为:(﹣1,0),
的坐标为:(﹣1,0),
∴-1是方程的一个根,
∴xp+(﹣1)=2+k,xp=3+k,
设直线BP的解析式为y=mx﹣3m,
∴![]() ,
,
∴![]() ,
,
∵点![]() 的坐标为:(3,0),
的坐标为:(3,0),
∴xp+3=m+2,xp=m-1,
∴3+k=m﹣1,
∴m﹣k=4,
设直线BQ的解析式为y=kx﹣3k,
∴Q(0,﹣3k),
∵R(0,﹣3m),
∴RQ=﹣3k+3m=12,
∵CO=3,
∴RQ=4OC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
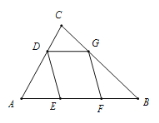
【题目】如图,在![]() 中,
中,![]() ,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y1=x2﹣4x+4的顶点为A,直线y2=kx﹣2k(k≠0),
(1)试说明直线是否经过抛物线顶点A;
(2)若直线y2交抛物线于点B,且△OAB面积为1时,求B点坐标;
(3)过x轴上的一点M(t,0)(0≤t≤2),作x轴的垂线,分别交y1,y2的图象于点P,Q,判断下列说法是否正确,并说明理由:
①当k>0时,存在实数t(0≤t≤2)使得PQ=3.
②当﹣2<k<﹣0.5时,不存在满足条件的t(0≤t≤2)使得PQ=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
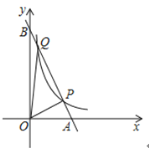
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() ,
,![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)直接写出![]() ,
,![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 与
与![]() 的面积相等吗?写出你的判断,并说明理由;
的面积相等吗?写出你的判断,并说明理由;
(3)若点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有3,4,5,x,甲,乙两人每次同时从袋中各随机取出1个小球,并计算2个小球上的数字之和.记录后将小球放回袋中搅匀,进行重复试验,试验数据如下表:
摸球总 次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出 现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出 现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果试验继续进行下去,根据上表提供的数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是________;
(2)如果摸出的2个小球上数字之和为9的概率是,那么x的值可以为7吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】粤东农批﹒2019球王故里五华马拉松赛于12月1日在广东五华举行,组委会为了做好运动员的保障工作,沿途设置了4个补给站,分别是:A(粤东农批)、B(奥体中心)、C(球王故里)和D(滨江中路),志愿者小明和小红都计划各自在这4个补给站中任意选择一个进行补给服务,每个补给站被选择的可能性相同.
(1)小明选择补给站C(球王故里)的概率是多少?
(2)用树状图或列表的方法,求小明和小红恰好选择同一个补给站的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com