
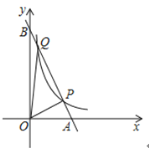
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() ,
,![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)直接写出![]() ,
,![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 与
与![]() 的面积相等吗?写出你的判断,并说明理由;
的面积相等吗?写出你的判断,并说明理由;
(3)若点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标.
的坐标.
科目:初中数学 来源: 题型:
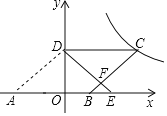
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限.将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=![]() (k≠0)图象经过点C,且S△BEF=
(k≠0)图象经过点C,且S△BEF=![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列四个条件:
①∠EBO=∠DCO;②BE=CD;③OB=OC;④OE=OD.
从上述四个条件中,选取两个条件,不能判定△ABC是等腰三角形的是:( )
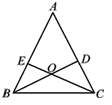
A. ①②B. ①③C. ③④D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
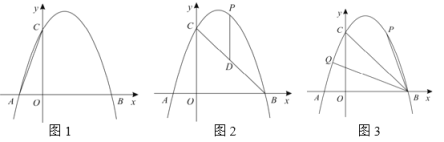
【题目】如图1,抛物线![]() 过点
过点![]() 轴上的
轴上的![]() 和
和![]() 点,交
点,交![]() 轴于点
轴于点![]() ,点
,点![]() 该物上限一点,且
该物上限一点,且![]() .
.
(1)抛物线的解析式为:____________;
(2)如图2,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,求点
,求点![]() 在运动的过程中线段
在运动的过程中线段![]() 长度的最大值;
长度的最大值;
(3)如图3,若![]() ,在对称轴左侧的抛物线上是否存在点
,在对称轴左侧的抛物线上是否存在点![]() ,使
,使![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是_____.①在同一平面内,a,b,c为直线,若a⊥b,b⊥c,则a∥c.②“若ac>bc,则a>b”的逆命题是真命题.③若M(a,2),N(1,b)关于x轴对称,则a+b=﹣1.④一个多边形的边数增加1条时,内角和增加180°,外角和不变.⑤![]() 的整数部分是a,小数部分是b,则ab=3
的整数部分是a,小数部分是b,则ab=3![]() ﹣3.
﹣3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
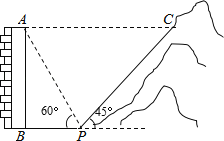
(1)若BP=10m,求居民楼AB的高度;(精确到0.1,![]() ≈1.732)
≈1.732)
(2)若PC=24m,求C、A之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间甲乙两商场搞促销活动,甲商场的方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”“20元”“30元”“50元”,顾客每消费满300元就可从箱子里不放回地摸出2个球,根据两个小球所标金额之和可获相应价格的礼品;乙商场的方案是:在一个不透明的箱子里放2个完全相同的小球,球上分别标“5元”“30元”,顾客每消费满100元,就可从箱子里有放回地摸出1个球,根据小球所标金额可获相应价格的礼品.某顾客准备消费300元.
(1)请用画树状图或列表法,求出该顾客在甲商场获得礼品的总价值不低于50元的概率;
(2)判断该顾客去哪个商场消费使获得礼品的总价值不低于50元机会更大?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
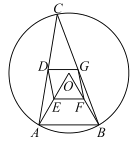
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com