
【题目】下列说法正确的是_____.①在同一平面内,a,b,c为直线,若a⊥b,b⊥c,则a∥c.②“若ac>bc,则a>b”的逆命题是真命题.③若M(a,2),N(1,b)关于x轴对称,则a+b=﹣1.④一个多边形的边数增加1条时,内角和增加180°,外角和不变.⑤![]() 的整数部分是a,小数部分是b,则ab=3
的整数部分是a,小数部分是b,则ab=3![]() ﹣3.
﹣3.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
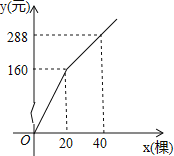
【题目】为更新树木品种,某植物园计划购进甲、乙两个品种的树苗栽植培育若计划购进这两种树苗共41棵,其中甲种树苗的单价为6元/棵,购买乙种树苗所需费用y(元)与购买数量x(棵)之间的函数关系如图所示.
(1)求出y与x的函数关系式;
(2)若在购买计划中,乙种树苗的数量不超过35棵,但不少于甲种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.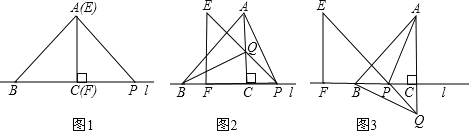
(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
(2)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
(3)若AC=BC=4,设△EFP平移的距离为x,当0≤x≤8时,△EFP与△ABC重叠部分的面积为S,请写出S与x之间的函数关系式,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的口袋中,分别有4个和3个大小、材质完全相同的小球,其中甲口袋中的小球上标有数字0,1,2,3,乙口袋中的小球上分别标有数字1,2,3,先从甲口袋中随机摸出一个小球,记下数字为![]() ,再从乙口袋中随机摸出一个小球,记下数字为
,再从乙口袋中随机摸出一个小球,记下数字为![]() .
.
(1)请用列表法或画树状图的方法表示出所有![]() 可能的结果;
可能的结果;
(2)规定:若![]() 都是方程
都是方程![]() 的解时,则小明获胜;若
的解时,则小明获胜;若![]() 都不是方程
都不是方程![]() 的解时,则小宇获胜,问他们两人谁获胜的概率大?
的解时,则小宇获胜,问他们两人谁获胜的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
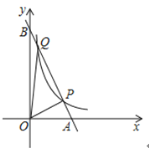
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() ,
,![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)直接写出![]() ,
,![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 与
与![]() 的面积相等吗?写出你的判断,并说明理由;
的面积相等吗?写出你的判断,并说明理由;
(3)若点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
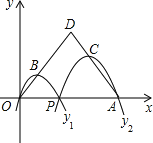
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于()
A.![]() B.
B.![]() C.3D.4
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
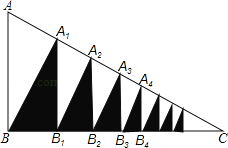
【题目】如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作A1B⊥AC,过A1作A1B1⊥BC,得阴影Rt△A1B1B;再过B1作B1A2⊥AC,过A2作A2B2⊥BC,得阴影Rt△A2B2B1;…如此下去.请猜测这样得到的所有阴影三角形的面积之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴于点
轴于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,与抛物线另一个交点为
,与抛物线另一个交点为![]() ,点
,点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方,且
上方,且![]() 是以
是以![]() 为腰的等腰三角形时,求点
为腰的等腰三角形时,求点![]() 的坐标;
的坐标;
(3)如图2,连接![]() ,以点
,以点![]() 为直角顶点,线段
为直角顶点,线段![]() 为较长直角边,构造两直角边比为1:2的
为较长直角边,构造两直角边比为1:2的![]() ,是否存在点
,是否存在点![]() ,使点
,使点![]() 恰好落在直线
恰好落在直线![]() 上?若存在,请直接写出相应点
上?若存在,请直接写出相应点![]() 的横坐标(写出两个即可);若不存在,请说明理由.
的横坐标(写出两个即可);若不存在,请说明理由.
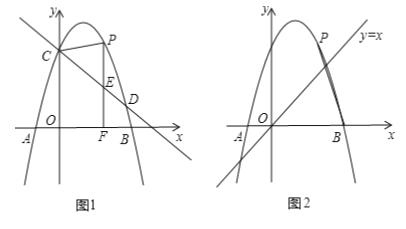
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com