
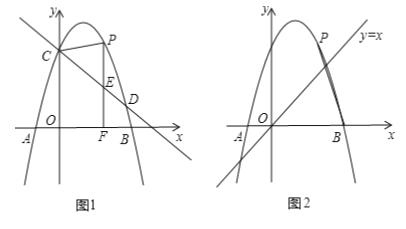
【题目】如图1,抛物线![]() 与
与![]() 轴于点
轴于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,与抛物线另一个交点为
,与抛物线另一个交点为![]() ,点
,点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方,且
上方,且![]() 是以
是以![]() 为腰的等腰三角形时,求点
为腰的等腰三角形时,求点![]() 的坐标;
的坐标;
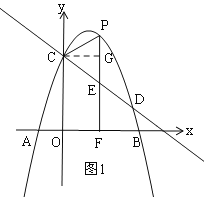
(3)如图2,连接![]() ,以点
,以点![]() 为直角顶点,线段
为直角顶点,线段![]() 为较长直角边,构造两直角边比为1:2的
为较长直角边,构造两直角边比为1:2的![]() ,是否存在点
,是否存在点![]() ,使点
,使点![]() 恰好落在直线
恰好落在直线![]() 上?若存在,请直接写出相应点
上?若存在,请直接写出相应点![]() 的横坐标(写出两个即可);若不存在,请说明理由.
的横坐标(写出两个即可);若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的坐标是
的坐标是![]() 或
或![]() ;(3)点
;(3)点![]() 的横坐标为-3或2或
的横坐标为-3或2或![]() 、
、![]() .
.
【解析】
(1)利用待定系数法即可求出二次函数的解析式;
(2)先把C点代入直线CD中求出m的值,表示P(m,-m2+2m+3)、E(m,-![]() m+3),
m+3),
当△CPE是以CE为腰的等腰三角形时,分两种情况:
①当CE=CP时,过C作CG⊥PF于G,根据OC=FG列方程解出即可;
②当CE=PE时,先表示CE、EG、CG的长,利用勾股定理得:CG2+EG2=CE2,列方程解出即可;
(3)先根据点P在抛物线上,G在直线y=x上设P(m,-m2+2m+3),G(a,a),
如图3,作辅助线,构建两个相似三角形,证明△PHG∽△BNP,则![]() ,由两直角边比为1:2列方程组解出横坐标m;
,由两直角边比为1:2列方程组解出横坐标m;
如图4,同理列方程组解出m的值.
解: ⑴将A(-1,0),C(0,3)代入![]() 得
得
![]()
解得:![]()
所以抛物线的解析式是![]() ;
;
⑵把![]() 代入直线
代入直线![]() 得:
得:![]() ,∴直线的解析式为:
,∴直线的解析式为:![]() ,
,
设![]() ,
,
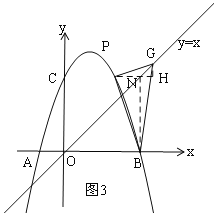
①当![]() 时,如上图,在图1中做辅助线,过
时,如上图,在图1中做辅助线,过![]() 作
作![]() 于
于![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,
,
②当![]() 时,在
时,在![]() 中,
中,![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,![]() ,解得:
,解得:![]() (舍),
(舍),![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,综上所述,当
,综上所述,当![]() 是以
是以![]() 为腰的等腰三角形时,点
为腰的等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() ;
;
(3)
设P(m,-m2+2m+3),G(a,a),
如图3,过B作BN∥y轴,过P作PH∥x轴,交于N,过G作GH⊥PN,垂足为H,则∠PHG=∠BNP=90°,
∴∠NBP+∠BPN=90°,
∵∠BPG=90°,
∴∠BPN+∠NPG=90°,
∴∠NBP=∠NPG,
∴△PHG∽△BNP,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
则![]() ,
,
解得:m1=-3,m2=2;
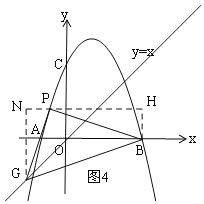
如图4,过P作NH∥x轴,过G作GN⊥NH,过B作BH⊥NH,垂足分别为N、H,
同理得:△PNG∽△BHP,
∴![]() ,
,
![]()
∴![]() 解得:m=
解得:m= ![]()
综上所述,相应点![]() 的横坐标为-3或2或
的横坐标为-3或2或![]() 、
、![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是_____.①在同一平面内,a,b,c为直线,若a⊥b,b⊥c,则a∥c.②“若ac>bc,则a>b”的逆命题是真命题.③若M(a,2),N(1,b)关于x轴对称,则a+b=﹣1.④一个多边形的边数增加1条时,内角和增加180°,外角和不变.⑤![]() 的整数部分是a,小数部分是b,则ab=3
的整数部分是a,小数部分是b,则ab=3![]() ﹣3.
﹣3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x与双曲线y=![]() (k>0,x>0)交于点A.过点A作AC⊥x轴于点C,过双曲线上另一点B作BD⊥x轴于点D,作BE⊥AC于点E,连接AB.若OD=3OC,则tan∠ABE=______.
(k>0,x>0)交于点A.过点A作AC⊥x轴于点C,过双曲线上另一点B作BD⊥x轴于点D,作BE⊥AC于点E,连接AB.若OD=3OC,则tan∠ABE=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
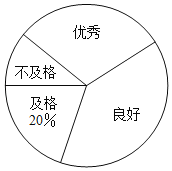
【题目】某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分.
成绩等级 | 频数(人) | 频率 |
优秀 | 15 | 0.3 |
良好 | ||
及格 | ||
不及格 | 5 |
根据以上信息,解答下列问题
(1)被测试男生中,成绩等级为“优秀”的男生人数为 人,成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 %;
(2)被测试男生的总人数为 人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 %;
(3)若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
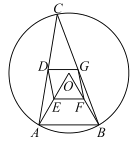
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
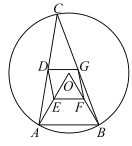
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师拿出四张卡片,背面完全一样,正面分别画有:矩形、菱形、等边三角形、圆背面朝上洗匀后先让小明抽出一张,记下形状后放回,洗匀后再让小亮抽出一张请你计算出两次都抽到既是中心对称图形又是轴对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
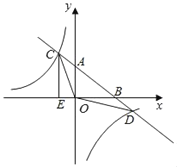
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=![]() ,OB=4,OE=1.
,OB=4,OE=1.
(1)求一次函数的解析式和反比例函数的解析式
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。
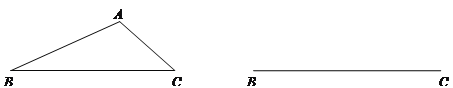
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com