
【题目】在平面直角坐标系xOy中,直线y=x与双曲线y=![]() (k>0,x>0)交于点A.过点A作AC⊥x轴于点C,过双曲线上另一点B作BD⊥x轴于点D,作BE⊥AC于点E,连接AB.若OD=3OC,则tan∠ABE=______.
(k>0,x>0)交于点A.过点A作AC⊥x轴于点C,过双曲线上另一点B作BD⊥x轴于点D,作BE⊥AC于点E,连接AB.若OD=3OC,则tan∠ABE=______.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.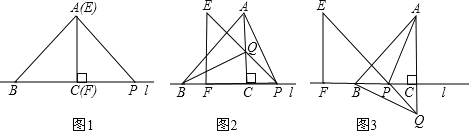
(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
(2)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
(3)若AC=BC=4,设△EFP平移的距离为x,当0≤x≤8时,△EFP与△ABC重叠部分的面积为S,请写出S与x之间的函数关系式,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作A1B⊥AC,过A1作A1B1⊥BC,得阴影Rt△A1B1B;再过B1作B1A2⊥AC,过A2作A2B2⊥BC,得阴影Rt△A2B2B1;…如此下去.请猜测这样得到的所有阴影三角形的面积之和为_____.
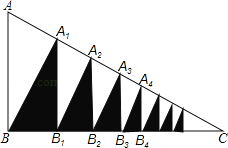
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育”是学校必须开展的一项重要工作.某校为了了解家长和学生参与“暑期安全知识学习”的情况,进行了网上测试,并在本校学生中随机抽取部分学生进行调查.若把参与测试的情况分为![]() 类情形:
类情形:![]() .仅学生自己参与;
.仅学生自己参与;![]() .家长和学生一起参与;
.家长和学生一起参与;![]() .仅家长自己参与;
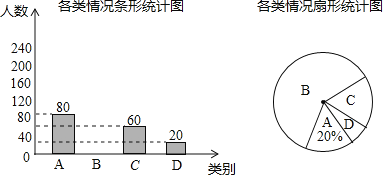
.仅家长自己参与;![]() .家长和学生都未参与.根据调查情况,绘制了以下不完整的统计图.请根据图中提供的信息,解答下列问题:
.家长和学生都未参与.根据调查情况,绘制了以下不完整的统计图.请根据图中提供的信息,解答下列问题:
![]() 在这次抽样调查中,共调查了 名学生;
在这次抽样调查中,共调查了 名学生;
![]() 补全条形统计图,并计算扇形统计图中
补全条形统计图,并计算扇形统计图中![]() 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;
![]() 根据抽样调查结果,估计该校
根据抽样调查结果,估计该校![]() 名学生中“家长和学生都未参与”的人数.
名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村启动“脱贫攻坚”项目,根据当地的地理条件,要在一座高为1000m的上种植一种经济作物.农业技术人员在种植前进行了主要相关因素的调查统计,结果如下:
①这座山的山脚下温度约为22°C,山高h(单位:m)每增加100m,温度T(单位:°C)下降约0.5°C;
②该作物的种植成活率p受温度T影响,且在19°C时达到最大.大致如表:
温度T°C | 21 | 20.5 | 20 | 19.5 | 19 | 18.5 | 18 | 17.5 |
种植成活率p | 90% | 92% | 94% | 96% | 98% | 96% | 94% | 92% |
③该作物在这座山上的种植量w受山高h影响,大致如图1:
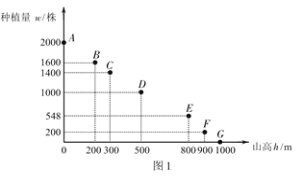
(1)求T关于h的函数解析式,并求T的最小值;
(2)若要求该作物种植成活率p不低于92%,根据上述统计结果,山高h为多少米时该作物的成活量最大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() 是
是![]() 上一点,点
上一点,点![]() 从点
从点![]() 沿折线
沿折线![]() 运动到点
运动到点![]() 时停止;点
时停止;点![]() 从点
从点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,速度均为每秒1个单位长度.如果点
时停止,速度均为每秒1个单位长度.如果点![]() ,
,![]() 同时开始运动,设运动时间为
同时开始运动,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,已知
,已知![]() 与
与![]() 的函数图象如图2所示,有以下结论:
的函数图象如图2所示,有以下结论:
①![]() ;
;
②![]() ;
;
③当![]() 时,
时,![]() ;
;
④当![]() 时,
时,![]() 是等腰三角形;
是等腰三角形;
⑤当![]() 时,
时,![]() .
.
其中正确的有( ).

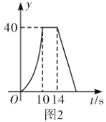
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
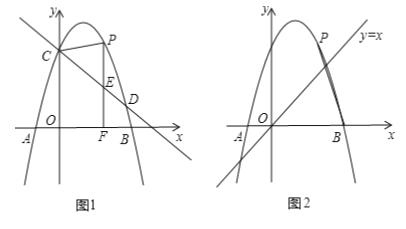
【题目】如图1,抛物线![]() 与
与![]() 轴于点
轴于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,与抛物线另一个交点为
,与抛物线另一个交点为![]() ,点
,点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方,且
上方,且![]() 是以
是以![]() 为腰的等腰三角形时,求点
为腰的等腰三角形时,求点![]() 的坐标;
的坐标;
(3)如图2,连接![]() ,以点
,以点![]() 为直角顶点,线段
为直角顶点,线段![]() 为较长直角边,构造两直角边比为1:2的
为较长直角边,构造两直角边比为1:2的![]() ,是否存在点
,是否存在点![]() ,使点
,使点![]() 恰好落在直线
恰好落在直线![]() 上?若存在,请直接写出相应点
上?若存在,请直接写出相应点![]() 的横坐标(写出两个即可);若不存在,请说明理由.
的横坐标(写出两个即可);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com