
【题目】某村启动“脱贫攻坚”项目,根据当地的地理条件,要在一座高为1000m的上种植一种经济作物.农业技术人员在种植前进行了主要相关因素的调查统计,结果如下:
①这座山的山脚下温度约为22°C,山高h(单位:m)每增加100m,温度T(单位:°C)下降约0.5°C;
②该作物的种植成活率p受温度T影响,且在19°C时达到最大.大致如表:
温度T°C | 21 | 20.5 | 20 | 19.5 | 19 | 18.5 | 18 | 17.5 |
种植成活率p | 90% | 92% | 94% | 96% | 98% | 96% | 94% | 92% |
③该作物在这座山上的种植量w受山高h影响,大致如图1:
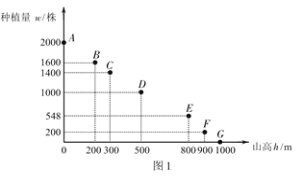
(1)求T关于h的函数解析式,并求T的最小值;
(2)若要求该作物种植成活率p不低于92%,根据上述统计结果,山高h为多少米时该作物的成活量最大?请说明理由.
【答案】(1)T=-![]() h+22(0≤h≤1000),当h=1000m时,T有最小值17°C;(2)山高h为300米时该作物的成活量最大.理由见解析.
h+22(0≤h≤1000),当h=1000m时,T有最小值17°C;(2)山高h为300米时该作物的成活量最大.理由见解析.
【解析】
(1)根据“这座山的山脚下温度约为22°C,山高h(单位:m)每增加100m,温度T(单位:°C)下降约0.5°C”,可以得出T关于h的函数解析式,根据T随h的增大而减小求T的最小值;
(2)成活率p与温度T之间的关系大致符合一次函数关系,先求出一次函数关系式;由图知,除点E外,其余点大致在一条直线上,然后求出一次函数关系式,最后求出成活量与h的函数关系式,从而确定山高h为300米时该作物的成活量最大.
解:(1)由题意得T=22-![]() ×0.5,
×0.5,
即T=-![]() h+22(0≤h≤1000).
h+22(0≤h≤1000).
∵-![]() <0,
<0,
∴T随h的增大而减小.
∴当h=1000m时,T有最小值17°C.
(2)根据表一的数据可知,当19≤T≤21时,成活率p与温度T之间的关系大致符合一次函数关系,不妨设p1=k1T+b1;
当17.5≤T<19时,成活率p与温度T之间的关系大致符合一次函数关系,不妨设p2=k2T+b2.
∵当T=21时,p1=0.9;当T=20时,p1=0.94,
解得: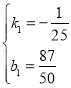 ,
,
∴ p1=-![]() T+
T+![]() (19≤T≤21).
(19≤T≤21).
∵当T=19时,p2=0.98;当T=18时,p2=0.94,
解得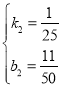 ,
,
∴p2=![]() T+
T+![]() (17.5≤T<19).
(17.5≤T<19).
由图知,除点E外,其余点大致在一条直线上,
因此,当0≤h≤1000时,可估计种植量w与山高h之间的关系大致符合一次函数关系,不妨设w=k3h+b3.
∵当h=200时,w=1600;当h=300时,w=1400,
解得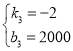 ,
,
∴w=-2h+2000(0≤h≤1000).
考虑到成活率p不低于92%,
则17.5≤T≤20.5
由T=-![]() h+22,可知T为17.5°C,19°C,20.5°C时,h分别为900m,600m,300m.
h+22,可知T为17.5°C,19°C,20.5°C时,h分别为900m,600m,300m.
由一次函数增减性可知:
当300≤h≤600时,p1=-![]() T+
T+![]() =-
=-![]() (-
(-![]() h+22)+
h+22)+![]() =
=![]() h+
h+![]() .
.
当600<h≤900时,p2=![]() T+
T+![]() =
=![]() (-
(-![]() h+22)+
h+22)+![]() =-
=-![]() h+
h+![]() .
.
∴当300≤h≤600时,
成活量=w·p1=(-2h+2000)·(![]() h+
h+![]() ).
).
∵-![]() <0,对称轴在y轴左侧,
<0,对称轴在y轴左侧,
∴当300≤h≤600时,成活量随h的增大而减小.
∴当h=300时,成活量最大.
根据统计结果中的数据,可知h=300时成活率为92%,种植量为1400株,
∴此时最大成活量为1400×92%=1288(株).
当600<h≤900时,
成活量=w·p2=(-2h+2000)·(-![]() h+
h+![]() ).
).
∵![]() >0,对称轴在h=900的右侧,
>0,对称轴在h=900的右侧,
∴当600<h≤900时,成活量随h的增大而减小.
且当h=600时,w·p1=w·p2
综上,可知当h=300时,成活量最大.
∴山高h为300米时该作物的成活量最大.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
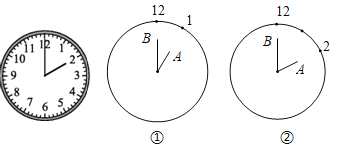
【题目】如图,有一时钟,时针OA长为6cm,分针OB长为8cm,△OAB随着时间的变化不停地改变形状.求:
(1)如图①,13点时,△OAB的面积是多少?
(2)如图②,14点时,△OAB的面积比13点时增大了还是减少了?为什么?
(3)问多少整点时,△OAB的面积最大?最大面积是多少?请说明理由.
(4)设∠BOA=α(0°≤α≤180°),试归纳α变化时△OAB的面积有何变化规律(不证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x与双曲线y=![]() (k>0,x>0)交于点A.过点A作AC⊥x轴于点C,过双曲线上另一点B作BD⊥x轴于点D,作BE⊥AC于点E,连接AB.若OD=3OC,则tan∠ABE=______.
(k>0,x>0)交于点A.过点A作AC⊥x轴于点C,过双曲线上另一点B作BD⊥x轴于点D,作BE⊥AC于点E,连接AB.若OD=3OC,则tan∠ABE=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
正方形内“奇妙点”及性质探究
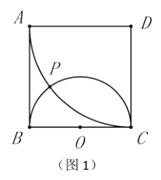
定义:如图1,在正方形![]() 中,以
中,以![]() 为直径作半圆
为直径作半圆![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,与半圆
,与半圆![]() 交于点
交于点![]() .我们称点
.我们称点![]() 为正方形
为正方形![]() 的一个“奇妙点”.过奇妙点的多条线段与正方形
的一个“奇妙点”.过奇妙点的多条线段与正方形![]() 无论是位置关系还是数量关系,都具有不少优美的性质值得探究.
无论是位置关系还是数量关系,都具有不少优美的性质值得探究.
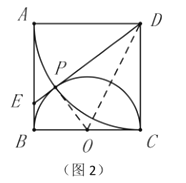
性质探究:如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则
,则![]() 为半圆
为半圆![]() 的切线.
的切线.
证明:连接![]() .
.
由作图可知,![]() ,
,
又![]() .
.
![]()
![]() ,∴
,∴![]() 是半圆
是半圆![]() 的切线.
的切线.
问题解决:
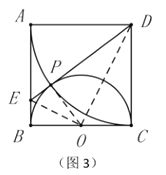
(1)如图3,在图2的基础上,连接![]() .请判断
.请判断![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)在(1)的条件下,请直接写出线段![]() 之间的数量关系;
之间的数量关系;
(3)如图4,已知点![]() 为正方形
为正方形![]() 的一个“奇妙点”,点
的一个“奇妙点”,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,请写出
,请写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;

(4)如图5,已知点![]() 为正方形
为正方形![]() 的四个“奇妙点”.连接
的四个“奇妙点”.连接![]() ,恰好得到一个特殊的“赵爽弦图”.请根据图形,探究并直接写出一个不全等的几何图形面积之间的数量关系.
,恰好得到一个特殊的“赵爽弦图”.请根据图形,探究并直接写出一个不全等的几何图形面积之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
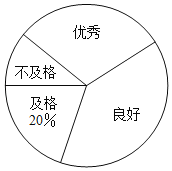
【题目】某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分.
成绩等级 | 频数(人) | 频率 |
优秀 | 15 | 0.3 |
良好 | ||
及格 | ||
不及格 | 5 |
根据以上信息,解答下列问题
(1)被测试男生中,成绩等级为“优秀”的男生人数为 人,成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 %;
(2)被测试男生的总人数为 人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 %;
(3)若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
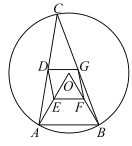
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com