
����Ŀ����ͼ����һʱ�ӣ�ʱ��OA��Ϊ6cm������OB��Ϊ8cm����OAB����ʱ��ı仯��ͣ�ظı���״����
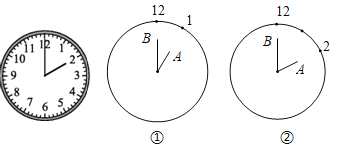
��1����ͼ�٣�13��ʱ����OAB������Ƕ��٣�
��2����ͼ�ڣ�14��ʱ����OAB�������13��ʱ�����˻��Ǽ����ˣ�Ϊʲô��
��3���ʶ�������ʱ����OAB���������������Ƕ��٣���˵�����ɣ�
��4�����BOA������0��ܦ���180�������Թ������仯ʱ��OAB������кα仯���ɣ���֤����
���𰸡���1��12cm2����2��14��ʱ��13��ʱ��OAB����������ˣ�����������3��3��ʱ����15ʱ����9��ʱ����21ʱ��ʱ��OAB��������24 cm2������������4��������0����180��ʱ�����������Σ���0��������90��ʱ��S��OAB��ֵ�������������90��������180��ʱ��S��OAB��ֵ�����������С
��������
��1����ͼ�٣�����B��BE��OA�ڵ�E����13��ʱ����BOA��30�������������ε������ʽ���ɵõ����ۣ�
��2����ͼ�ڣ�����B��BE��OA�ڵ�E����14��ʱ����BOA��60����![]() ��sin60����BE��8��
��sin60����BE��8��![]() ��4
��4![]() ��cm�������������ε������ʽ���ɵõ����ۣ�
��cm�������������ε������ʽ���ɵõ����ۣ�
��3��3��ʱ����15ʱ����9��ʱ����21ʱ��ʱ��OAB����������ͼ�ۢܣ����������ε������ʽ���ɵõ����ۣ�
��4��������0����180��ʱ�����������Σ���0��������90��ʱ��S��OAB��ֵ�������������90��������180��ʱ��S��OAB��ֵ�����������С��
�⣺��1����ͼ�٣�����B��BE��OA�ڵ�E��
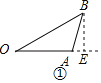
��13��ʱ����BOA��30����
��BE��![]() OB��4��cm����
OB��4��cm����
��S��OAB��![]() OABE��
OABE��![]() ��6��4��12��cm2����
��6��4��12��cm2����
��2����ͼ�ڣ�����B��BE��OA�ڵ�E��
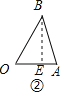
��14��ʱ����BOA��60����![]() ��sin60����BE��8��
��sin60����BE��8��![]() ��4
��4![]() ��cm����
��cm����
��S��OAB��![]() ��4
��4![]() ��6��12
��6��12![]() ��cm2����
��cm2����
��12![]() ��12��
��12��
��14��ʱ��13��ʱ��OAB����������ˣ���3��3��ʱ����15ʱ����9��ʱ����21ʱ��ʱ��OAB����������ͼ�ۢܣ�
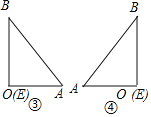
�ߴ�ʱBE���BE��OB��8 cm����OA���䣬
��S��![]() OAOB��
OAOB��![]() ��6��8��24��cm2����
��6��8��24��cm2����
��4��������0����180��ʱ�����������Σ�
�ٵ�0��������90��ʱ����Խ��OA���䣬OA���ϵĸ�Խ��Խ��
��S��OAB��ֵ�������������
�ڵ�90��������180��ʱ��OA���䣬��OA���ϵĸ�Խ��ԽС��
��S��OAB��ֵ�����������С��
������������0��������90��ʱ��S��OAB��ֵ�������������90��������180��ʱ��S��OAB��ֵ�����������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����Ƹһ��Ա������ӦƸ�ס��ҡ��������ӱ��ԡ������������������������.�ס��ҡ�����������÷����±���(��λ����)
�� | �� | �� | �� | |
���� | 86 | 92 | 80 | 90 |
���� | 90 | 88 | 94 | 84 |
��1����4��ѡ�ֱ��Գɼ�����λ���� �֣����Ե�ƽ������ ��.
��2���ù�˾�涨�����ԡ����Էֱ�40%��60%�ı��������ܷ֣��Ҹ���ɼ������õ���85��. ���ݹ涨������˵��˭����¼��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼס������������Ŀڴ��У��ֱ���4����3����С��������ȫ��ͬ��С�����мڴ��е�С���ϱ�������0��1��2��3���ҿڴ��е�С���Ϸֱ��������1��2��3���ȴӼڴ����������һ��С��������Ϊ![]() ���ٴ��ҿڴ����������һ��С��������Ϊ
���ٴ��ҿڴ����������һ��С��������Ϊ![]() ��
��
��1�������б�������״ͼ�ķ�����ʾ������![]() ���ܵĽ����
���ܵĽ����
��2���涨����![]() ���Ƿ���
���Ƿ���![]() �Ľ�ʱ����С����ʤ����
�Ľ�ʱ����С����ʤ����![]() �����Ƿ���
�����Ƿ���![]() �Ľ�ʱ����С���ʤ������������˭��ʤ�ĸ��ʴ�
�Ľ�ʱ����С���ʤ������������˭��ʤ�ĸ��ʴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
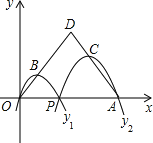
����Ŀ����ͼ����֪��A��4��0����OΪ����ԭ�㣬P���߶�OA������һ�㣨�����˵�O��A������P��O����Ķ��κ���y1��P��A����Ķ��κ���y2��ͼ�ھ����£����ǵĶ���ֱ�ΪB��C������OB��AC�ཻ�ڵ�D����OD=AD=3ʱ�����������κ��������ֵ֮�͵��ڣ���
A.![]() B.
B.![]() C.3D.4
C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
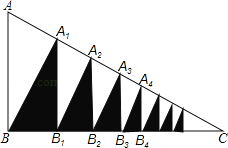
����Ŀ����ͼ����Rt��ABC�У�AB��3��BC��4����ABC��90������B��A1B��AC����A1��A1B1��BC������ӰRt��A1B1B���ٹ�B1��B1A2��AC����A2��A2B2��BC������ӰRt��A2B2B1���������ȥ����²������õ���������Ӱ�����ε����֮��Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�Rt��OAB�Ķ���A��x����������ϣ�����B������Ϊ(3��![]() )����C������Ϊ(1��0)����PΪб��OB�ϵ�һ���㣬��PA+PC����Сֵ_____��
)����C������Ϊ(1��0)����PΪб��OB�ϵ�һ���㣬��PA+PC����Сֵ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���B������Ϊ��4��2����ֱ��y=��![]() x+
x+![]() ���AB��BC�ֱ��ཻ�ڵ�M��N������y=
���AB��BC�ֱ��ཻ�ڵ�M��N������y=![]() ��x��0����ͼ�����M��
��x��0����ͼ�����M��
��1����˵����NҲ�ں���y=![]() ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��2����ֱ��MN��y��ĸ�����ƽ�Ƶõ�ֱ��M��N�䣬��ֱ��M��N���뺯��y�T![]() ��x��0����ͼ�����һ������ʱ����ֱ��M'N��Ľ���ʽ��
��x��0����ͼ�����һ������ʱ����ֱ��M'N��Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������ƶ���ᡱ��Ŀ�����ݵ��صĵ���������Ҫ��һ����Ϊ1000m������ֲһ�־������ũҵ������Ա����ֲǰ��������Ҫ������صĵ���ͳ�ƣ�������£�
������ɽ��ɽ�����¶�ԼΪ22��C��ɽ��h����λ��m��ÿ����100m���¶�T����λ����C���½�Լ0.5��C��
�ڸ��������ֲ�ɻ���p���¶�TӰ�죬����19��Cʱ�ﵽ����������
�¶�T��C | 21 | 20.5 | 20 | 19.5 | 19 | 18.5 | 18 | 17.5 |
��ֲ�ɻ���p | 90% | 92% | 94% | 96% | 98% | 96% | 94% | 92% |
�۸�����������ɽ�ϵ���ֲ��w��ɽ��hӰ�죬������ͼ1��
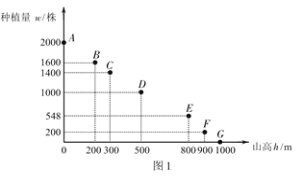
��1����T����h�ĺ�������ʽ������T����Сֵ��
��2����Ҫ���������ֲ�ɻ���p������92%����������ͳ�ƽ����ɽ��hΪ������ʱ������ijɻ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
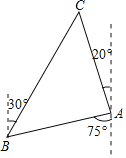
����Ŀ����ͼ��һ���洬λ�ڵ���A����ƫ��75�㷽���B��������A��30����洬�ر�ƫ��30�㷽��Ѱ��Ⱥ������һ��ʱ�����λ��A����ƫ��20�㷽���C�����洬�����˹������������ڵ���A����Ѳ�ߴ���������źţ�Ѳ�ߴ��յ��źź���40����ÿСʱ���ٶ�ǰ������������Ѳ�ߴ����ٷ����ܹ�����C�������ο����ݣ�![]() ��1.4��sin40���0.64��cos40���0.77��tan40���0.84���������ȷ��1���ӣ���
��1.4��sin40���0.64��cos40���0.77��tan40���0.84���������ȷ��1���ӣ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com