
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 | 86 | 92 | 80 | 90 |
面试 | 90 | 88 | 94 | 84 |
(1)这4名选手笔试成绩的中位数是 分,面试的平均数是 分.
(2)该公司规定:笔试、面试分别按40%,60%的比例计入总分,且各项成绩都不得低于85分. 根据规定,请你说明谁将被录用.
科目:初中数学 来源: 题型:
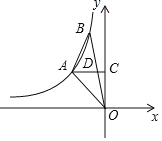
【题目】如图,A、B是反比例函数![]() 图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红为了更直观了解“物体质量”的概念,各选五个鸡蛋称重,以每个![]() 为标准,大于或等于
为标准,大于或等于![]() 即为达标,超过标准部分的克数记为正数,不足标准部分的克数记为负数.小明所统计的数据为实际称重读数,小红为记录数据,把所得数据整理成如下统计表(单位:
即为达标,超过标准部分的克数记为正数,不足标准部分的克数记为负数.小明所统计的数据为实际称重读数,小红为记录数据,把所得数据整理成如下统计表(单位:![]() ).
).
序号 数据 姓名 | 1 | 2 | 3 | 4 | 5 |
小明 | 48 | 50 |
| 49 | 51 |
小红 |
|
|
| 2 | 1 |
经过统计发现,小明所选鸡蛋质量的平均数为![]() ,小红所选鸡蛋质量的众数为
,小红所选鸡蛋质量的众数为![]() ,根据以上信息:
,根据以上信息:
(1)填空:![]() ,
,![]() ;
;
(2)通过计算说明,小明和小红哪个选取的鸡蛋大小更均匀,请说明理由;
(3)现从小明和小红所选取的鸡蛋里各随机挑一个,这两个鸡蛋质量都达标的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
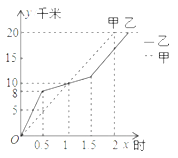
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图象信息,下列说法:①两人相遇前,甲速度一直小于乙速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的说法是_________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
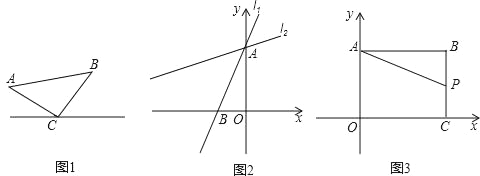
【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
实践操作:过点A作AD⊥l于点D,过点B作BE⊥l于点E,求证:△CAD≌△BCE.
模型应用:(1)如图2,在直角坐标系中,直线l1:y=![]() x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的个数有( )
①若 x2+kx+25 是一个完全平方式,则 k 的值等于 10;
②一组对边平行,一组对角相等的四边形是平行四边形;
③顺次连接平行四边形的各边中点,构成的四边形是菱形;
④黄金分割比的值为![]() ≈0.618.
≈0.618.
A. 0 个 B. 1 个 C. 2 个 D. 3 个
查看答案和解析>>
科目:初中数学 来源: 题型:
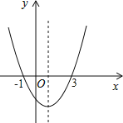
【题目】如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:
①ab<0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;
④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;
⑥3a+2c<0.
其中不正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
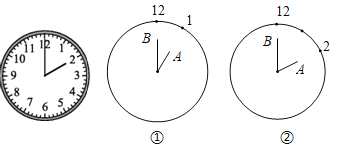
【题目】如图,有一时钟,时针OA长为6cm,分针OB长为8cm,△OAB随着时间的变化不停地改变形状.求:
(1)如图①,13点时,△OAB的面积是多少?
(2)如图②,14点时,△OAB的面积比13点时增大了还是减少了?为什么?
(3)问多少整点时,△OAB的面积最大?最大面积是多少?请说明理由.
(4)设∠BOA=α(0°≤α≤180°),试归纳α变化时△OAB的面积有何变化规律(不证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com