
【题目】下列命题正确的个数有( )
①若 x2+kx+25 是一个完全平方式,则 k 的值等于 10;
②一组对边平行,一组对角相等的四边形是平行四边形;
③顺次连接平行四边形的各边中点,构成的四边形是菱形;
④黄金分割比的值为![]() ≈0.618.
≈0.618.
A. 0 个 B. 1 个 C. 2 个 D. 3 个
科目:初中数学 来源: 题型:
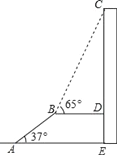
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
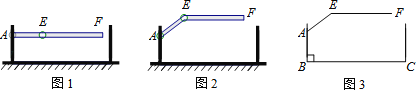
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+3)x+m2=0有两个不相等的实数根,
(1)求m的取值范围
(2)若α,β是方程的两个实数根,且满足![]() =﹣1,求m的值.
=﹣1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
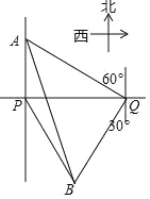
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向, B位于南偏西30°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
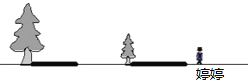
【题目】两棵树(大树和小树)在一盏路灯下的影子如图所示
(1)确定路灯灯泡的位置(用点P表示)和表示婷婷的影长的线段(用线段AB表示).
(2)若小树高为2m,影长为4m;婷婷高1.5m,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
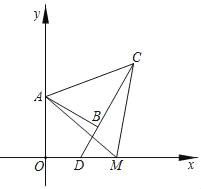
【题目】如图,在平面直角坐标系中,已知A(0,2),M(m,0)且m>0,分别以AO、AM为边在∠AOM内部作等边△AOB和等边△AMC,连接CB并延长交x轴于点D,则C点的横坐标的值为( )
A. ![]() m+
m+![]() B.
B. ![]() m+
m+![]() C.
C. ![]() m+
m+![]() D.
D. ![]() m+
m+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在△ABC中,AB=AC,点 D 是边 BC 的中点.以BD为直径作⊙O,交边 AB于点P,连接PC,交AD于点E.
(1)求证:AD是⊙O的切线;
(2)当∠BAC=90°时,求证:CE=2PE;
(3)如图2,当PC是⊙O的切线,E为AD 中点,BC=8,求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com