练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

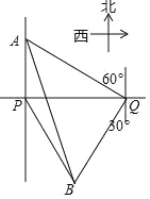
    【题目】一轮船在P处测得灯塔A在正北方向，灯塔B在南偏东30°方向，轮船向正东航行了900m，到达Q处，测得A位于北偏西60°方向， B位于南偏西30°方向．

    （1）线段BQ与PQ是否相等？请说明理由；

    （2）求A、B间的距离（结果保留根号）．

    【答案】（1）相等；（2）

    【解析】试题分析：（1）由题意知∠QPB=60°、∠PQB=60°，从而得△BPQ是等边三角形，据此可得答案；

    （2）由（1）知PQ=BQ=900m，从而得AQ=，根据∠AQB=180°-60°-30°=90°知AB=（m）．

    试题解析：（1）相等，由图知∠QPB=60°、∠PQB=60°，

    ∴△BPQ是等边三角形，∴BQ=PQ；

    （2）由（1）知PQ=BQ=900m，在Rt△APQ中，AQ=，

    又∵∠AQB=180°﹣60°﹣30°=90°，

    ∴在Rt△AQB中，AB=（m），

    答：A、B间的距离为300m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】聪聪参加我市电视台组织的“阳光杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有个选项，第二道单选题有4个选项，这两道题聪聪都不会，不过聪聪还有两个“求助”可以用（使用“求助”一次可以让主持人去掉其中一题的一个错误选项）．

    （1）如果聪聪两次“求助”都在第一道题中使用，那么聪聪通关的概率是　 　．

    （2）如果聪聪将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

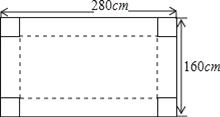
    【题目】我国水资源比较缺乏，人均水量约为世界人均水量的四分之一，其中西北地区缺水尤为严重．一村民为了蓄水，他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水．已知白铁皮的长为280cm，宽为160cm（如图）．

    （1）若水箱的底面积为16000cm2，请求出切去的小正方形边长；

    （2）对（1）中的水箱，若盛满水，这时水量是多少升？（注：1升水=1000cm3水）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y1=﹣x+4，y2=x+b都与双曲线y=交于点A（1，m），这两条直线分别与x轴交于B，C两点．

    （1）求y与x之间的函数关系式；

    （2）直接写出当x＞0时，不等式x+b＞的解集；

    （3）若点P在x轴上，连接AP把△ABC的面积分成1：3两部分，求此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，得到A，B的对应点C，D，连接AC，BD，CD.

    (1)直接写出点C，D的坐标，求出四边形ABDC的面积；

    (2)在x轴上是否存在一点F，使得三角形DFC的面积是三角形DFB面积的2倍，若存在，请求出点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点 O 是等边△ABC 内一点，∠AOB＝105°，∠BOC 等于α，将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC，连接 OD.

    （1）求证：△COD 是等边三角形．

    （2）求∠OAD 的度数．

    （3）探究：当α为多少度时，△AOD 是等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，AB＝AC，∠BAC＝90°，D为AC边上一动点，且不与点A点C重合，连接BD并延长，在BD延长线上取一点E，使AE＝AB，连接CE．

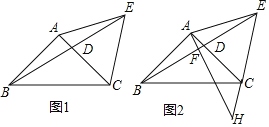
    （1）若∠AED＝20°，则∠DEC＝　 　度；

    （2）若∠AED＝a，试探索∠AED与∠AEC有怎样的数量关系？并证明你的猜想；

    （3）如图2，过点A作AF⊥BE于点F，AF的延长线与EC的延长线交于点H，求证：EH2+CH2＝2AE2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P在第一象限，△ABP是边长为2的等边三角形，当点A在x轴的正半轴上运动时，点B随之在y轴的正半轴上运动，运动过程中，点P到原点的最大距离是______；若将△ABP的PA边长改为，另两边长度不变，则点P到原点的最大距离变为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

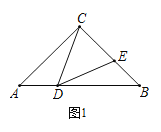
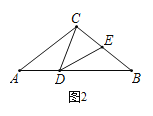
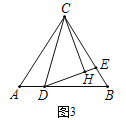
    【题目】如图，在等腰△ABC中，AC＝BC，D，E分别为AB，BC上一点，∠CDE＝∠A．

    （1）如图1，若BC＝BD，∠ACB＝90°，则∠DEC度数为_________°；

    （2）如图2，若BC＝BD，求证：CD＝DE；

    （3）如图3，过点C作CH⊥DE，垂足为H，若CD＝BD，EH＝1，求DE－BE的值．

    查看答案和解析>>

    同步练习册答案