
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

【答案】(1)证明见解析;(2)45°;(3)105°,127.5°或 150°.
【解析】(1)由旋转的性质得到△BCO≌△ACD, 再由全等三角形对应边相等得到OC=CD,根据有一个角为60°的等腰三角形是等边三角形即可得出结论;
(2)由等边三角形的性质、三角形内角和定理以及旋转的性质即可得出结论.
(3)若△AOD 是等腰三角形 ,分三种情况讨论即可.
(1)∵△BOC 旋转 60°得到△ADC,∴△BCO≌△ACD,
∴OC=CD,且∠OCD=60°,则△OCD 是等边三角形;
(2)∵△ABC 为等边三角形,∴∠BAO+∠OAC=60°,∠ABO+∠OBC=60°.
∵∠AOB=105°,∴∠BAO+∠ABO=75°,∴∠OAC+∠OBC=120°﹣105°=45°.
∵△BOC 旋转 60°得到△ADC,∴△BCO≌△ACD,
∴∠DAC=∠OBC ,∴∠OAD=∠OAC+∠CAD=45°.
(3)若△AOD 是等腰三角形 .∵由(1)知△OCD 是等边三角形,∴∠COD=60°.
由(2)知∠OAD=45°, 分三种情况讨论:
①当 OA=OD 时,∠AOD=90°,∠α=360°﹣105°﹣60°﹣90°=105°;
②当 OA=AD 时,∠AOD=67.5°,∠α=360°﹣105°﹣60°﹣67.5°=127.5°;
③当 AD=OD 时,∠AOD=45°,∠α=360°﹣105°﹣60°﹣45°=150°.
综上所述:当α=105°,127.5°或 150°时,△AOD 是等腰三角形 .


科目:初中数学 来源: 题型:
【题目】观察下面的变形规律:
![]() ;
;![]() ;
;![]() ;….
;….
解答下面的问题:
(1)仿照上面的格式请写出![]() = ;
= ;
(2)若n为正整数,请你猜想![]() = ;
= ;
(3)基础应用:计算:![]() .
.
(4)拓展应用1:解方程:![]() =2016
=2016
(5)拓展应用2:计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
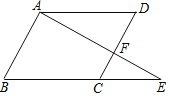
【题目】如图,若∠DAE=∠E,∠B=∠D,那么AB∥DC吗?请在下面的解答过程中填空或在括号内填写理由.
解:理由如下:
∵∠DAE=∠E,________
∴______∥BE,________
∴∠D=∠DCE.________
又∵∠B=∠D,________
∴∠B=______.(等量代换)
∴______∥______,(同位角相等,两直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ//BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )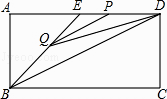
A.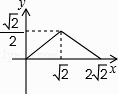
B.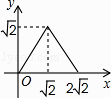
C.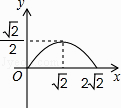
D.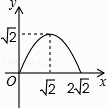
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.

(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com