
【题目】两棵树(大树和小树)在一盏路灯下的影子如图所示
(1)确定路灯灯泡的位置(用点P表示)和表示婷婷的影长的线段(用线段AB表示).
(2)若小树高为2m,影长为4m;婷婷高1.5m,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.
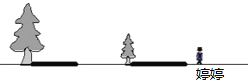
【答案】(1)见解析(2)路灯灯泡的高度为10.5m
【解析】
(1)根据中心投影的特点可知,连接物体和它影子的顶端所形成的直线必定经过点光源.所以分别把两棵树的顶端和影子的顶端连接并延长可交于一点,即点光源的位置,连接PC并延长交QA的延长线与点B,即可得;
(2)由DF∥PQ得△DEF∽△QEP,根据相似三角形的性质有![]() ,即
,即![]() ①,同理可得
①,同理可得![]() ,即
,即![]() ②,联立①②可得PQ.
②,联立①②可得PQ.
(1)如图,点P即为灯泡所在位置;
线段AB即为婷婷的影长;

(2)如图,由题意知,DF=2,DE=4,DA=10,AC=1.5,AB=4.5,
∵DF∥PQ,
∴△DEF∽△QEP,
∴![]() ,即
,即![]() ①,
①,
∵CA∥PQ,
∴△CAB∽△PQB,
∴![]() ,即
,即![]() ②,
②,
由①②可得PQ=10.5,
答:路灯灯泡的高度为10.5m.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
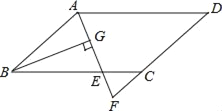
A. 8 B. 9.5 C. 10 D. 11.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为________海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为________海里/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的个数有( )
①若 x2+kx+25 是一个完全平方式,则 k 的值等于 10;
②一组对边平行,一组对角相等的四边形是平行四边形;
③顺次连接平行四边形的各边中点,构成的四边形是菱形;
④黄金分割比的值为![]() ≈0.618.
≈0.618.
A. 0 个 B. 1 个 C. 2 个 D. 3 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 y=﹣x+2 与反比例函数 y=![]() (k≠0)的图象交于 A(a,3)、B(3,b)两点,直线 AB 交 y 轴于点 C、交 x 轴于点 D.
(k≠0)的图象交于 A(a,3)、B(3,b)两点,直线 AB 交 y 轴于点 C、交 x 轴于点 D.
(1)请直接写出 a=_______,b=______,反比例函数的解析式为_______.
(2)在 x 轴上是否存在一点 E,使得∠EBD=∠OAC,若存在请求出点 E 的坐标, 若不存在,请说明理由.
(3)点P 是 x 轴上的动点,点 Q 是平面内的动点,是以 A、B、P、Q 为顶点的四边形是矩形,若存在请求出点 Q 的坐标,若不存在请说明理由.
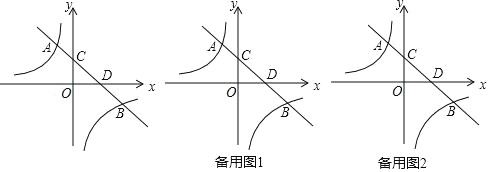
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠ACB=30°
(1)如图1,当AB=AC=2,求BC的值;
(2)如图2,当AB=AC,点P是△ABC内一点,且PA=2,PB=![]() ,PC=3,求∠APC的度数;
,PC=3,求∠APC的度数;
(3)如图3,当AC=4,AB=![]() (CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为 .
(CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
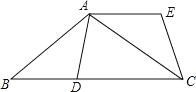
【题目】如图,在△ABC 中,AB=AC.D 是 BC 上一点,且 AD=BD.将△ABD 绕点 A 逆时针旋转得到△ACE.
(1)求证:AE∥BC;
(2)连结 DE,判断四边形 ABDE 的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com